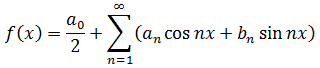■ 「フーリエ変換」に関する知識を学ぶ!
普段の生活には全く縁がないと思われる数学知識ですが、市場分析という
世界に足を踏み入れたのであれば無関係とは言えない知識になるでしょう。
参考書買っても中身がさっぱり理解できない・・ (ノ_・。)
あ~どうやって理解したらいいのかなぁ・・
諦めよっかなぁ・・
と知識の取得を諦めてしまう方も多いことでしょう。当コンテンツは、そんな方々
へお贈りいたします。
■ 今回扱う知識は「ある関数にフーリエ級数を適用する」
【常に過去の記事内容を把握!】
当ブログにおけるフーリエ変換の解説はExcelで体験したフーリエ変換にて出力
された値を再現していく方式で解説していきます。
よってExcelの分析ツールによるフーリエ変換が行えるようにしておいてください。
解説には時間がかかるのでExcelの分析ツールでフーリエ変換を繰り返して使い
方を慣れておくと良いかもしれませんね (^-^)/
一応、過去の記事へのリンクを載せておきます!
参考 : 知識0でフーリエ変換をしてみる
参考 : フーリエ変換とは何に変換されるのか?
参考 : 逆フーリエ変換にて各領域を行き来する
参考 : フーリエ変換と周波数成分
参考 : フーリエ級数から理解していく
参考 : フーリエ級数と直交
参考 : フーリエ級数と偶・奇関数
参考 : 【超重要】波の基礎知識
参考 : ある関数とフーリエ級数
【フーリエ級数を積分して係数 a0 を求める】
前回はフーリエ級数の数式をちょっと変形した式まで扱いました。必ず変形
する必要はないのですが解説がわかり易くなるだろうということで変形した次
第です。念のために変形前のフーリエ級数と変形後のフーリエ級数の数式
を載せておきます。
・ 変形前
そして、このフーリエ級数は「ある関数f(x)が三角関数で表現することが可能」と
いう意味を持つと前回解説しましたが、
各種係数(a0 an bn)が導けないと解けない ( p_q)
のですねえ。ということで今回は各係数を導くためのプロセスを解説します。この
プロセスは難しいものではなく、
「-π~π」の区間で積分する Σ(゚д゚;)
ことで各係数を求めるのです。プロセスの中でCosやSinを両辺に乗じたりして複雑
に思えてしまうかもしれませんが可能な限り丁寧に解説していきますね (^-^)/
【両辺共に-π~π区間で積分をする】
最初に求める係数は 「a0」 となります。この係数を求めるには変形したフーリエ級
数の両辺を-π~πで積分することで導かれます。では積分した式をみてみましょう!
上段の数式は一端両辺に積分をしたもので、下段は右辺を項別にしたものです。ど
ちらも同じ意味となります。フーリエ級数の数式を変形したのは項別に表示するのを
スムーズにしたかっただけなのですね (;^_^A
イメージ的に理解が早い部分から積分していきましょうか♪
CosとSinは「-π~π」の区間で積分すると「0」となります。これは図をみれば一目瞭
然です。Sinは上下に対称なので即理解できますよね。Cosはわかり難いかもしれない
ので色を塗ってあります。
ということで残るは a0 の積分ですが、 a0 は実は定数なのですよ。なので
積分は簡単で微分して 1/2*a0 になる形にして-π~πの定積分を行えば良
いのですねえ。積分についてわからない方は下記記事を参考にしてください!
参考 : 積分の計算
ということで計算ができますよね (^-^)/
そして a0 で整理しますと係数 a0 の公式が導かれます。
ここまでは高校数学の積分初級範囲なので比較的簡単だと思います。次に
係数 an、bn を求めていくことになりますが基本的には三角関数の公式に
従う高校数学の範囲です。フーリエ級数が難しいように思えるのは、
基本となる高校数学の集合体 (ノ゚ο゚)ノ
であるからでしょう。高校数学までは三角関数なら三角関数、波なら波と個別
に覚えていくだけで、あらゆる知識を複合的に考えることは多くありません。そ
んなことから、あらゆる知識を動員するものに対して難しさを覚えてしまうわけ
です。応用とは各種基本の複合体であると考えれば基本の大切さってのがわ
かりますよね ('-^*)/