マイクラ記事です。
回路の解説をちゃんとやるって難しいですね…
さて、今回作ってみたのは、タイトル通り(タイトルめっちゃなげぇ…)。
ま、割と簡単にできる回路です。
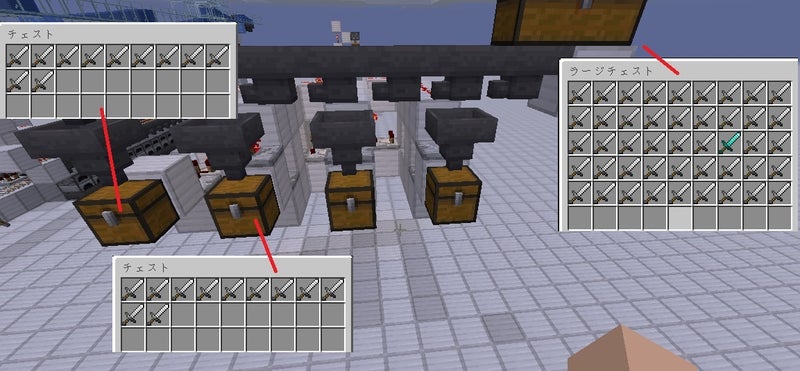
まずは外観から。
こんな感じです。
機能面を説明しましょう。
ラージチェストに入れた大量のアイテムを、
複数の(スモール)チェストに均等に分配するような機構を考えてみました。
どこで役に立つんだよってのは、さておき…
「均等」の意味を正確にしておきましょう。
チェストの中身を検知するコンパレーターから出る信号強度が
同じになるような「均等」なので、ぴったりと均等に分割されるわけではありません。
どういうことかと説明すると、
すべてのスモールチェストが空の状態では、
ラージチェストの中身は、ホッパーの緑色で印された道を通っていきます。
このとき、赤丸で囲ったホッパーは全てロックされています。
なので、1番のチェストにのみアイテムが入っていきます。
次いで、1番のチェストを検知しているコンパレーターから、
信号強度1のレッドストーン信号が出たとき、つまりチェストの容量の 1/16 が満たされたとき、
2番のチェストの上のホッパーのロックが解除され、アイテムは2番に流れます。
以下同様に、2番が 1/16 満たされれば、3番のホッパーが解除され、アイテムは3番に。
3番が満たされれば、アイテムが4番に流れていきます。
全てのチェストの容量が、1/16 を満たしたときには、
また1番のチェストにアイテムが流れるようになります。
そして、1番のチェストが 2/16 満たされれば、次は2番のチェストが 2/16 になる。
以下同様です。
回路部分を上から。
拡張性があり、チェストをさらに増やすこともできるんですが、
チェストを増やすたびに回路が横に広がっていっちゃうんですよね…。
もっと小さくできないかなぁ…
この回路から…
オレンジ色で囲った部分を取り除いてみます。
オレンジ色の下の部分はこんな風になっています。
水色の線は、
取り除かれた部分が、レッドストーントーチをリピーターに繋げていることを示しています。
リピーターは、チェストのすぐ上にあるホッパーをロックしています。
ま、コンパレーターだらけの回路ですね。
基本的には、同じような回路の繰り返しなので、最小単位に分解しますと…
こんな感じです。
AとBのチェストの中身を比較し、Aの中身>Bの中身となった場合、
トーチが消えるように組みました。
地味にコンパレーターの性質をフルに活かした機構かなーって思っています。
この回路を作る時に、ハッキリ意識できたことがひとつあります。
それは、コンパレーターの減算モードと比較モードの違いですね。
比較される信号が同等のとき、比較モードでは信号を流すんですが、
減算モードでは、信号が0になる。
まぁ、当たり前っちゃ当たり前なんですが、
比較モードは、後ろからの入力信号=横からの入力信号の場合、
そのまま後ろからの入力信号を流します。
減算モードでは、後ろからの入力-横からの入力=0になるので、
消えるってわけですね。
この回路には、減算のほうが都合のいいので、
こちらを採用しています。
まー四等分までなら、この装置で良いと思うんですけどね…。
回路で作ってみました。
ちなみに、紹介した機構は…
大型のかまど機構を作ってみている試作段階で、
「こういう回路があったらいいな」と思って考えたものです。
赤丸の部分にアイテムを均等に分配する機構を取り付けてみました。
かまど機構自体は、見てのとおりちょっと複雑なんですが、
まぁうまくいってるとは思ってないので、今後作り直しを考えています。