こんばんは。
若菜塾 数学講師の平野くりえです。
今日は、中1数学【空間図形】転がした円錐の表面積 について
1問解説したいと思います。
よろしくお願いします。
(問題)
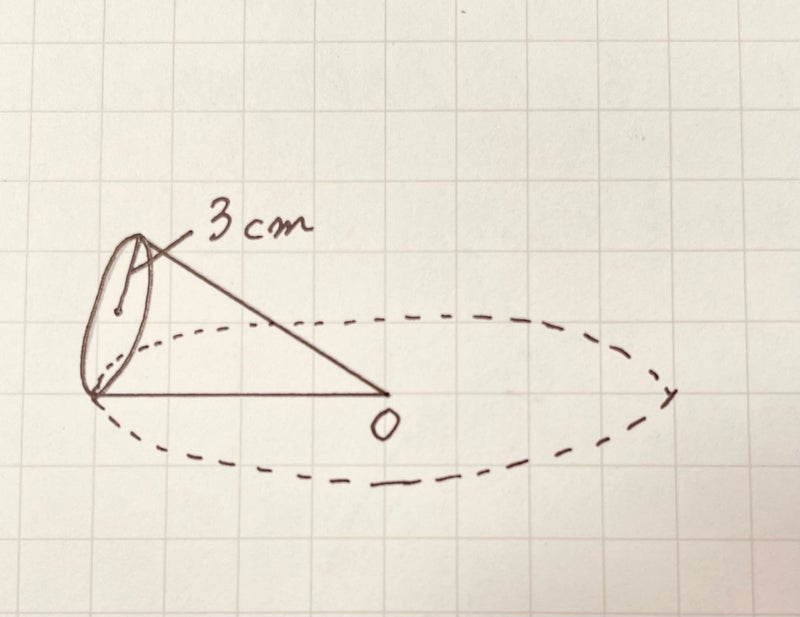
図のように、底面の半径が3㎝の円錐を、頂点Oを固定して転がしたところ、ちょうど3回転してもとの位置に戻った。このとき、この円錐の表面積を求めなさい。
(解き方)
ポイントは、円錐の表面積の求め方と
円の周の長さの求め方です。
円錐の表面積
円の周の長さ
円錐の表面積を求めるためには
母線の長さが必要です。
母線の長さは、この図でみると頂点Oを中心とした円の半径になっています。(円Oとします。)
ですので、円Oの半径を求めます。
円Oとは、円錐を転がした跡でつくられた円です。
円錐を3回転させて円Oがつくられているので
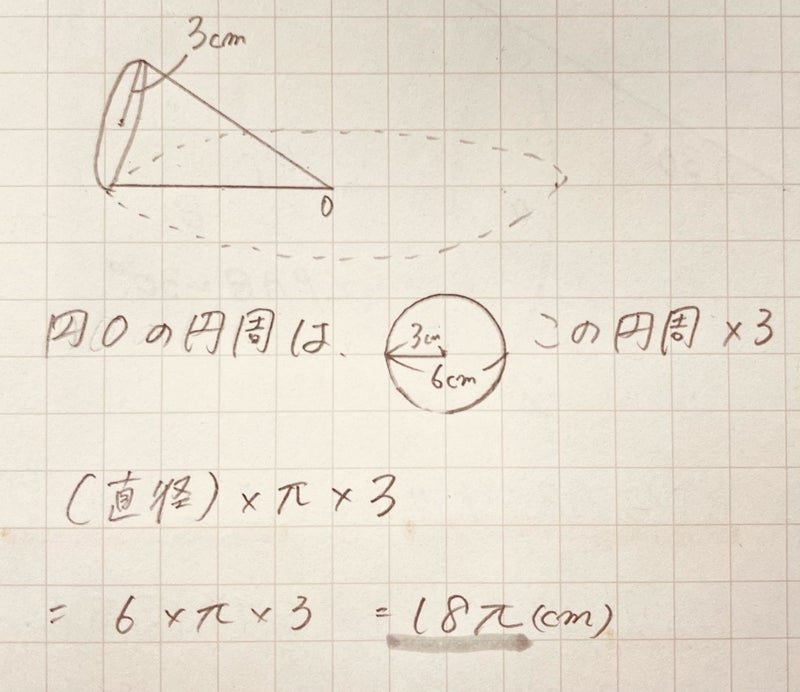
円Oの円周は、円錐の底面の円周×3 ということになります。
円Oの円周がわかれば、
(直径)×π で円周なので、円Oの直径 がわかります。
つまり、直径÷2で 半径がわかります。
答えは 36π㎠ です。
空間図形では、たまに見かける問題ですが
私は結構好きな問題です。
円錐の底面の半径が3㎝ という情報から、いろいろな長さを求め、円錐の表面積を出す ところまでたどり着く
問題を解いていく楽しさがあるように感じます。
平野くりえの数学blogでした。