ねじの真直度（ねじの曲がり）
JIS B1021のネジの曲がりについて、備忘録的に。
ねじの曲がりについては、JIS B1021 3.2.2.2真直度の図48にあります。
ねじのMDに対して、部品等級Ａ，Ｂの場合
─|φt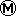
≦8 t=0.002×l+0.05
＞8 t=0.0025×l+0.05
(lは首下長さ)
となっています。10mmに対して70um。
ちょっとマージンあれば問題ないですが、当然ながらねじも曲がってるんですね。
ねじの曲がりについては、JIS B1021 3.2.2.2真直度の図48にあります。
ねじのMDに対して、部品等級Ａ，Ｂの場合
─|φt
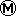
≦8 t=0.002×l+0.05
＞8 t=0.0025×l+0.05
(lは首下長さ)
となっています。10mmに対して70um。
ちょっとマージンあれば問題ないですが、当然ながらねじも曲がってるんですね。
ねじへの最大実体公差方式（MMR）の適用
ねじ、ねじ穴グループへの最大実体公差方式（MMR）の適用
軸や穴のグループへ最大実体公差方式（MMR、JIS B0023）を指定することはイメージしやすいのですが、その軸や穴がねじの場合（つまり形状としてはギザギザの軸や穴）の場合はどのように定義されるでしょうか。
普通の穴へMMRを適用した場合は、径が大きく仕上がればそのぶん幾何公差を追加できます（JIS B0023）。これはわかりやすいですね。ではねじ穴の場合は？めねじ内径が大きく仕上がっていても、めねじ谷の径が小さく仕上がっていれば、幾何公差を追加できるんでしょうか？できるならどれだけ追加できるのでしょうか？
これにはポイントがふたつあります。
① ねじに対する幾何公差は、特に指定しなければピッチ円筒（有効径円筒）に適用される。意図に応じておねじ外形やめねじ内径を指定できる（JIS B0021 10.2）
② ねじ部品の最大実体寸法（JIS B0023）は、JISのねじなら、ねじ山形（各種径）に対する公差（JIS B0209）とねじ部品の真直度に対する公差（JIS B1021）から与えられる
①について
特に指定しない場合、つまりねじのかみ合い具合が関係する場合は、幾何公差はピッチ円筒に適用されるとあります。検証はねじつきのゲージで検証します。例としてJIS B0021 付属書C図19にゲージの例があります。
ねじのかみ合い具合は関係なくて、たとえばおねじを貫通穴を通すような場合には、「MD」を図面に指示することによって外形寸法を指定することができます。
つまり、意図によってねじへの最大実体公差の指示方法は変える必要があります。
②について
JISねじの最大実体寸法はねじ山径サイズだけではなく、幾何公差は別に与えられているので注意が必要です。
いずれにしても、最大実体公差方式を適用する際には、検証するための機能ゲージがどのようにあるべきかを考えないと意図とずれた指定をしてしまいそうですね。私も修行が必要。
＜参考記事＞
ねじ穴への最大実体公差方式（MMR）の適用（失敗）
軸や穴のグループへ最大実体公差方式（MMR、JIS B0023）を指定することはイメージしやすいのですが、その軸や穴がねじの場合（つまり形状としてはギザギザの軸や穴）の場合はどのように定義されるでしょうか。
普通の穴へMMRを適用した場合は、径が大きく仕上がればそのぶん幾何公差を追加できます（JIS B0023）。これはわかりやすいですね。ではねじ穴の場合は？めねじ内径が大きく仕上がっていても、めねじ谷の径が小さく仕上がっていれば、幾何公差を追加できるんでしょうか？できるならどれだけ追加できるのでしょうか？
これにはポイントがふたつあります。
① ねじに対する幾何公差は、特に指定しなければピッチ円筒（有効径円筒）に適用される。意図に応じておねじ外形やめねじ内径を指定できる（JIS B0021 10.2）
② ねじ部品の最大実体寸法（JIS B0023）は、JISのねじなら、ねじ山形（各種径）に対する公差（JIS B0209）とねじ部品の真直度に対する公差（JIS B1021）から与えられる
①について
特に指定しない場合、つまりねじのかみ合い具合が関係する場合は、幾何公差はピッチ円筒に適用されるとあります。検証はねじつきのゲージで検証します。例としてJIS B0021 付属書C図19にゲージの例があります。
ねじのかみ合い具合は関係なくて、たとえばおねじを貫通穴を通すような場合には、「MD」を図面に指示することによって外形寸法を指定することができます。
つまり、意図によってねじへの最大実体公差の指示方法は変える必要があります。
②について
JISねじの最大実体寸法はねじ山径サイズだけではなく、幾何公差は別に与えられているので注意が必要です。
いずれにしても、最大実体公差方式を適用する際には、検証するための機能ゲージがどのようにあるべきかを考えないと意図とずれた指定をしてしまいそうですね。私も修行が必要。
＜参考記事＞
ねじ穴への最大実体公差方式（MMR）の適用（失敗）
ヘリカルカーブ/スパイラルカーブの関係式でのコントロール
ヘリカルカーブ/スパイラルカーブの関係式でのコントロール
ヘリカルカーブ/スパイラルカーブを関係式でコントロールしようと思って、ヘリカルカーブ フィーチャーをダブルクリックして寸法を編集するときの注意点です。
ヘリカルカーブの定義方法には、
・ピッチと回転
・高さと回転
・高さとピッチ
・スパイラル
の4種類があります。デフォルトでは「ピッチと回転」ですが、「ピッチと回転」で定義されている時にも、フィーチャーをダブルクリックすると「高さ」寸法が出てきます。
てっきり高さをコントロールしても反映されるのかなと思いますが、この状態で高さ寸法を変更しても（あるいは、関係式を追加しても）反映されません。
高さでコントロールしたいときには、定義を「高さとピッチ」に変更するとうまくいきます。
あるいはそのままピッチと回転でコントロールしたい場合は、出てくる高さは無視して、ピッチと回転（数）（直線パターンと同じように小さく出てくる）だけを変更したり、関係式に追加するとうまくいきます。
ヘリカルカーブ/スパイラルカーブを関係式でコントロールしようと思って、ヘリカルカーブ フィーチャーをダブルクリックして寸法を編集するときの注意点です。
ヘリカルカーブの定義方法には、
・ピッチと回転
・高さと回転
・高さとピッチ
・スパイラル
の4種類があります。デフォルトでは「ピッチと回転」ですが、「ピッチと回転」で定義されている時にも、フィーチャーをダブルクリックすると「高さ」寸法が出てきます。
てっきり高さをコントロールしても反映されるのかなと思いますが、この状態で高さ寸法を変更しても（あるいは、関係式を追加しても）反映されません。
高さでコントロールしたいときには、定義を「高さとピッチ」に変更するとうまくいきます。
あるいはそのままピッチと回転でコントロールしたい場合は、出てくる高さは無視して、ピッチと回転（数）（直線パターンと同じように小さく出てくる）だけを変更したり、関係式に追加するとうまくいきます。
ゼロ公差（ゼロ幾何公差）でGo！（？）
JIS B0023の話題を書いたので、ゼロ公差の話題を少し。
その前にこのブログ内でもゼロ公差ゼロ公差言ってましたけど、ゼロ幾何公差が正しいですね。無知をひけらかしてしまってすいません。以上言い訳（になってない）。
ゼロ公差方式は最大実体公差方式（記号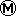）のような、寸法公差と幾何公差が関連する方式の一種で、最初に幾何公差に割り当てられるぶんをぜんぶ寸法公差に割り当ててしまい、幾何公差をゼロにするやり方です。JIS B0023の7にあります。
たとえば、穴径φ4.1～4.3、位置度φ0.1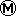としていたところを、φ4.0～4.3の位置度φ0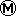とします。
こうすることで位置度公差ぶん穴径の許容サイズを広げることができます。が、意図は変わっていないので実質同じ事です。よりリーズナブルな公差設定と言えます。
問題は、「公差ゼロって何考えとんじゃこのゆとりが！」と思われないか心配なことです。
あと個人的には、寸法数値（上記の例ではφ4.1～4.3、±で書くと4.2±0.1）の中心値が変わってしまう（4.15±0.15になる）のがなんとな～くきもちわるいことです。
なのでなんとな～く使いづらい。
この原因はおそらく普段CADCADしてるからで、もっと現実の物を見るようにすれば呪縛から逃れられるかなと思うんですが、なかなか…とにかくまだ今のところはなんとな～くきもちわるいです。
その前にこのブログ内でもゼロ公差ゼロ公差言ってましたけど、ゼロ幾何公差が正しいですね。無知をひけらかしてしまってすいません。以上言い訳（になってない）。
ゼロ公差方式は最大実体公差方式（記号
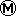）のような、寸法公差と幾何公差が関連する方式の一種で、最初に幾何公差に割り当てられるぶんをぜんぶ寸法公差に割り当ててしまい、幾何公差をゼロにするやり方です。JIS B0023の7にあります。たとえば、穴径φ4.1～4.3、位置度φ0.1
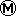としていたところを、φ4.0～4.3の位置度φ0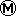とします。こうすることで位置度公差ぶん穴径の許容サイズを広げることができます。が、意図は変わっていないので実質同じ事です。よりリーズナブルな公差設定と言えます。
問題は、「公差ゼロって何考えとんじゃこのゆとりが！」と思われないか心配なことです。
あと個人的には、寸法数値（上記の例ではφ4.1～4.3、±で書くと4.2±0.1）の中心値が変わってしまう（4.15±0.15になる）のがなんとな～くきもちわるいことです。
なのでなんとな～く使いづらい。
この原因はおそらく普段CADCADしてるからで、もっと現実の物を見るようにすれば呪縛から逃れられるかなと思うんですが、なかなか…とにかくまだ今のところはなんとな～くきもちわるいです。
公差方式が明記されてない図面の公差解釈（JIS）
●公差方式が明記されてない図面の公差解釈
公差表示方式 JIS B 0024(ISO 8015)
書かれてますか？書いてない場合もありますよね。
JIS B0024では、B0024の公差方式を適用する場合、表題欄付近に「公差表示方式 JIS B0024」を表記するよう定めていますが、書いてない場合はどう読むのでしょうか？
JIS B0401-1 5.3 公差付き寸法の解釈
のところで、JIS B0024の公差方式について書かれています。特に指定がなければ独立の原則（幾何形状は寸法公差から独立＝規制を受けない）です。
そして5.3.2にて、JIS B0024の注記がない場合について書かれています。
ここで、まず、
（規格の文章はまどろっこしいのでやや意訳します）
穴の場合：最大内接完全円筒径が最大実体許容寸法(=許容最小径)より小さいとダメ
軸の場合：最小外接完全円筒径が最大実体許容寸法(=許容最大径)より小さいとダメ
両方小さいとダメ です。
つまり穴の場合は、包絡の条件と同じ(最大実体境界を違反しない)ですが、軸の場合は最大実体境界を違反（あるいは、ぴったり）しないといけないみたいです。
これじゃ穴と軸がはまりません(汗)
これはおそらく包絡の条件（B0024 6.1）をあらわすつもりだったと思われますが、どうやら間違っているようです。そういうわけで、読むときには包絡の条件で読めばよいと思いますが、自分が書くときには、この文章を引用元にして包絡の条件を主張することはちょっとできないので、包絡の条件をデフォルトで適用する場合でも
・B0024を指定した上で、
・一般公差クラス指定に、包絡の条件を示す"-E"をつける（B0419 6.3)
ようにしています。
（2009-10-22 書き直して再掲しました）
（2009-12-13 書き直して再掲／追記）
対応するISO規格 ISO286-1:1988では、5.3.2の表記が正しく包絡の条件の内容になっていました。つまり、軸の場合「大きいとダメ(should not be larger than)」でした。JISが誤訳のようです。
●関連記事
公差方式が明記されてない図面の公差解釈（ISO）
公差表示方式 JIS B 0024(ISO 8015)
書かれてますか？書いてない場合もありますよね。
JIS B0024では、B0024の公差方式を適用する場合、表題欄付近に「公差表示方式 JIS B0024」を表記するよう定めていますが、書いてない場合はどう読むのでしょうか？
JIS B0401-1 5.3 公差付き寸法の解釈
のところで、JIS B0024の公差方式について書かれています。特に指定がなければ独立の原則（幾何形状は寸法公差から独立＝規制を受けない）です。
そして5.3.2にて、JIS B0024の注記がない場合について書かれています。
ここで、まず、
（規格の文章はまどろっこしいのでやや意訳します）
穴の場合：最大内接完全円筒径が最大実体許容寸法(=許容最小径)より小さいとダメ
軸の場合：最小外接完全円筒径が最大実体許容寸法(=許容最大径)より小さいとダメ
両方小さいとダメ です。
つまり穴の場合は、包絡の条件と同じ(最大実体境界を違反しない)ですが、軸の場合は最大実体境界を違反（あるいは、ぴったり）しないといけないみたいです。
これじゃ穴と軸がはまりません(汗)
これはおそらく包絡の条件（B0024 6.1）をあらわすつもりだったと思われますが、どうやら間違っているようです。そういうわけで、読むときには包絡の条件で読めばよいと思いますが、自分が書くときには、この文章を引用元にして包絡の条件を主張することはちょっとできないので、包絡の条件をデフォルトで適用する場合でも
・B0024を指定した上で、
・一般公差クラス指定に、包絡の条件を示す"-E"をつける（B0419 6.3)
ようにしています。
（2009-10-22 書き直して再掲しました）
（2009-12-13 書き直して再掲／追記）
対応するISO規格 ISO286-1:1988では、5.3.2の表記が正しく包絡の条件の内容になっていました。つまり、軸の場合「大きいとダメ(should not be larger than)」でした。JISが誤訳のようです。
●関連記事
公差方式が明記されてない図面の公差解釈（ISO）