2023年
立命館大学・全学文系
数学 Ⅰ
おはようございます。ますいしいです![]()
受験生の皆さんの健闘を心より応援しております![]()
今回の下の問題,
〔3〕[テ]は,なかなか
難しいですね![]()
さて,どうしよう……![]()
それでは,最初は解答を見ずにチャレンジしてみてください![]()
(問題)
(※ 時間の目安)〔1〕5分 〔2〕5分 〔3〕12分 ![]()
〔1〕Relation between roots and coefficients
〔2〕Coordinate plane
〔3〕Plane vector
(ますいしいの解答)
コメント;いかがでしたでしょうか?楽しんで頂けましたでしょうか?
〔1〕超頻出の問題です![]() また,出題されます
また,出題されます![]()
確実に,Get できるようにしておきましょう![]()
〔2〕(1)は微分でも行けますが,ここでは,“逆たどり法”で
導出してみました![]()
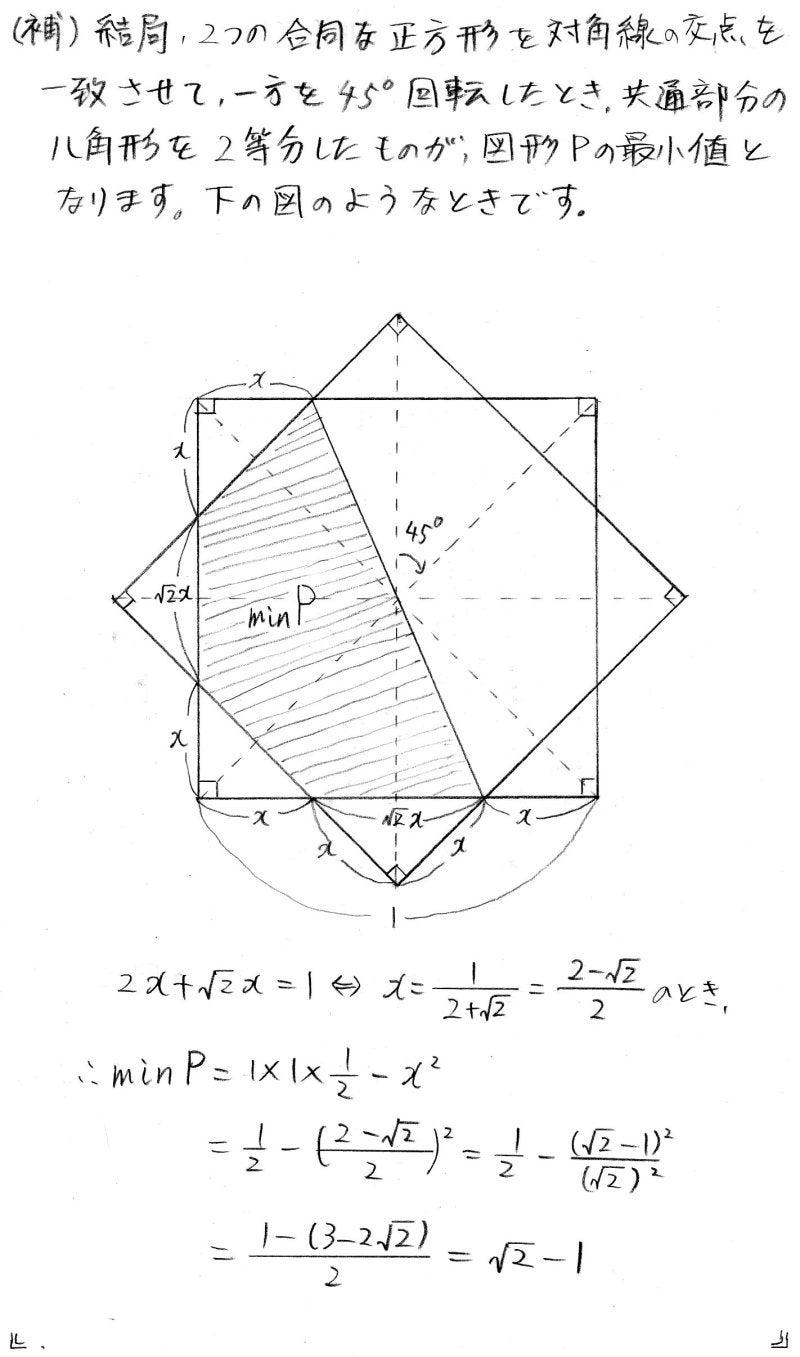
〔3〕最後の[テ]は,時間内には厳しいか![]()
それでは、次回をお楽しみに![]()
by ますいしい