体感する数学セミナー が終わりました。
こんにちは。
数学学芸員のようじです。
体感する数学セミナーが終わりました。
今回は６名の方にお越し頂きました。
しかもお一人は高校２年生！！
京都大学の数学科を目指しているそうです。
ぜひ現役合格してほしいものです。
今回のセミナーでは「人の造りし数」についてお話しました。
自然数、整数、有理数、無理数、超越数、実数、虚数、複素数のお話から始まり
・有理数の稠密性（ちょうみつせい）
・デテキントの切断
・超越数
そして、代表的な美しい数として
・黄金比
・円周率
もお話しました。
もちろん「ラマヌジャンパイ」も紹介しました！
全体的にちょっと難しくなってしまいました。
数学初心者の方か数学をある程度知っている方、どちらに合わせるか迷ってしまい、
結局どっちつかずになってしまいました。
ターゲッティングは大切ですね。
（セミナーでは比較的易しい話に特化し、もっと知りたい方をブログに誘えばいいのですね。）
数秘術に詳しい方がいらっしゃって、最初の自己紹介で語っていらっしゃいました。
ちなみに私の誕生数は２２です！
セミナーにいらっしゃった方には、当日使用したパワーポイントを差し上げています。
ラマヌジャンパイも今回参加してくださった方には差し上げようと思います。
次回は１１月２１日（日）お金数学セミナーです。
今から楽しみです(^ ^)
ありがとうございました。
素敵な分数です。
こんにちは。
数学学芸員のようじです。
今日は久々に数学美術をご紹介します。
芸術的というよりもトリックアートのようなものかもしれません。
ぜひ、何が潜んでいるか探してみてくださいね。
フェルマーの最終定理 －ピュタゴラスに始まり、フェルマーが証明するまで サイモン・シン
数学学芸員のようじです。
今日は数学本の紹介です。
新潮社
売り上げランキング: 14701
この本は私が初めて数学に感動をした本です。
大学時代にこの本に出会い、フェルマーの最終定理が証明されるまでのドラマを知りました。
そのドラマは、あまりに壮大で感動に満ち溢れたものでした。
（きっと映画化しても楽しめる！）
難しい数式は全くなく、ドラマチックな感動を素直に感じられる本です。
フェルマーの最終定理にたどり着くまでに歴史上の数学者が考えてきた問題（数論やパズルなど）も紹介されていて、数学の神秘や楽しさを１冊でたくさん体感できます。
このあまりに壮大なストーリーをぜひ読んでみてください！！
無限について ～濃度と連続体仮説～
こんにちは。
数学学芸員のようじです。
いよいよ「無限について」最後のお話です。
可算無限集合⇒自然数、整数、有理数、有理数方程式の解の集合・・・などなど
非加算無限集合⇒無理数、超越数・・・などなど
でした。
可算無限集合を記号で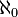
（アレフゼロ）と表します。
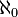は無限の濃度の一番小さいものであり、このアレフゼロよりも小さい濃度はすべて有限集合になります。
また、非加算無限集合のうち、無理数や超越数といったものは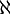
（アレフ）といいます。
ここである人はひょんなことを考えました。
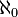「と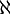の間の濃度ってあるの？(´･ω･`)」
これが連続体仮説です。
結果をお話しますと、連続体仮説はゲーデルの不完全性定理の代表例として扱われているように、
「真か偽か証明できない」ことが証明されています。
自然数と実数の間の濃度があるかどうかを我々は証明することができないのですね。
シリーズでお話してきた無限。
最初にお話しましたように、無限は想像するだけで怖い気がします。
それだけ恐ろしいもの。
無限の取り扱いには十分にご注意くださいね！
無限について ～カントールの対角線論法～
こんにちは。
数学学芸員のようじです。
無限の話もだんだんと終わりに近づいてきました。
今日ご紹介するのは、無限の話で最も大切な
カントールの対角線論法です。
これを理解して、周りの人に語れるようになれば、アナタも立派な無限通です！
さて、自然数と整数、有理数がすべて１：１対応できて、同じ濃度であることを勉強しました。
では実数はどうでしょうか？？
自然数と０から１の実数では、どちらの濃度が大きいか（はたまた同じか）を調べます。
材料）
・背理法
・カントールの対角線論法
背理法とは、
「こうなるのでは？」と仮定して、話をすすめていくと矛盾が出てきて、「やっぱり最初の仮定が違うんだ」とする証明法です。
では、まず
０から１の実数すべてに自然数で番号をつけられる（すべて１：１対応できる）と仮定しましょう。
番号をつけられたとすると、以下のように並べられます。
（０から１の実数すべてに①、②、③、④・・・と自然数番号をつけられるとしています。画像で並べている小数は適当です。）
でも、すべての実数に番号をつけたと思っても、
このように、①、②、③、④のそれぞれの小数点第○位の数より少し違う数を各小数点桁に並べて作った実数は、自然数番号をつけたどの実数にも該当しません。
すなわち、０から１のすべての実数に自然数番号をつけられたと仮定したのですが、それでも番号のついていない新しい実数を作ってしまうことができるのです。
これはすべての０から１の実数に自然数番号をつけたという仮定に反します。
以上より、０から１の実数すべてに自然数で番号をつけられるという仮定が間違っていたことになります。
よって、０から１の実数は自然数よりも濃度が大きいのです。
これがカントールの対角線論法です。
非常にすっきりシンプルに０から１の実数のほうが自然数よりも濃度が濃いことを証明できました。
さすがカントールさん！
０から１という有限の長さの中に、無限に続く自然数よりも多い点があるのですね。
（まぁ、自然数は高々加算ですしね！）
実は、０から１の実数と実数全体は同じ濃度です。
これらの無限集合を非可算無限集合（Uncountable infinity set)といいます。
（余談）
有理数が可算無限集合で、実数全体が非可算無限集合ということですので、
実は無理数（実数から有理数をひいたもの）が非可算無限集合なのです。
もっというと、実は有理数係数の代数方程式の解となる数は可算無限で、解とならない数（超越数）は非加算無限なのです！！！
次回はいよいよ
アレフゼロや連続体仮説、ゲーデルの不完全性定理をお話します！( ﾟ∀ﾟ)ﾉ