気体の分子運動論

　先日の三重での物理教育の研修会で、気体の分子運動論の授業がうまく行かないという相談を受けました。
　高校の物理の教科書では、ちょっと程度が高い内容なので、普通に講義すると、聞いてもわからない、難しくて根を上げる、寝てしまう・・・のいずれかになりがちな内容で、ぼくは講義形式ではなく、双方向のやりとりで行っていると答えました。
　でも、詳しくは話せなかったので、この場を利用して、お答えしておきたいと思います。

　そもそも、気体の分子運動論の内容は、クラウジウスやマクスウェル（上図）が統計数学を用いて導いた論文の内容をもとにしていますから、高校生にとってはかなりハイレベルな内容になっています。

　そこには、通常の物理では扱わないΣの計算なども登場しますし、個々の分子の運動と平均的な運動をどう関連づけるかという高度な内容も入ってきます。さらに、分子のでたらめな運動をどのように数式で表すかという、高校生のレベルをはるかに超える考え方も登場します。

　普通にやったら、よほど物理が好きで数学の能力も高い生徒でなければ、ついてこられません。

　それなのに、教科書には必ず載っているし、大学入試にも頻繁に出題されます。

　それは、気体の分子運動論が、理論物理学の象徴的な内容だからです。

　分子が動いて壁にぶつかっているというモデルから、紙と鉛筆だけで理論計算を進めることで、温度の正体が見えてくるのだから、自然科学の本質的な探究心を大いに刺激する感動的な教材といえます。

　さらに、運動量と力積、気体の状態方程式、運動エネルギーやモルの概念など、基本的な物理知識を組み合わせて解く問題になりますから、高校物理の基礎力を総合的に試すこともできます。

　そりゃあ、大学入試に出題したくなりますよね。

　でも、最初に述べたように、これだけ程度が高く、しかも複雑な行程の内容を、講義形式でとうとうと説明した場合、高校生にとっては聞いてすぐに理解できる内容にはなりません。

　ぼくが教育実習生の頃に見学した授業の中に、この分子運動論の授業がありました。教室の生徒がみな困惑した表情のまま、長い講義にひたすら耐えている様子が印象的でした。

　進学校といわれる学校でこれなんですから、フツーの学校で同じ講義をやられてはたまりません。１時間のところを２時間、３時間とかけて、ゆっくり丁寧に説明しても、考査で出題すると、だれもできません。これでは、講義した意味がありません。

　そんなわけで、ぼくは分子運動論の授業を一方的な講義形式で行うことは、長い間行っていません。

　分子運動論の内容を理解し、定着するのには、もっとアクティブな授業形式が適しています。

　幸い、分子運動論は、論理構成としては、単純ないくつかのパートの積み重ねできています。

　その中で、生徒の予備知識としてないものは、一カ所だけ・・・分子の熱運動の乱雑さをどう数式に表現するかというところだけです。（この内容が高校生のレベルを超えるものであることは、大学の出題者はよくわかっていて、ほとんどの入試問題では、この部分は問題文の中に与えられています）

　それ以外は、物理や数学の授業ですでに習っている内容ばかり。

　したがって、講義として受動的に聞くより、総合的な復習問題として、各自で挑戦する形式の方が、生徒にとってもやる気がわくし、理解度や定着率も高くなります。

　では、分子運動論の理論構成を、パートごとに見ていきましょう。

パート１：気体分子と壁との衝突を運動量と力積の関係を用いて調べ、一つの分子が壁に及ぼす力の平均値を求める。

　力学の基本知識が必要です。

　ぼくは、最初の導入として、知的好奇心を刺激する問題を示し、生徒との質疑応答をしています。

（問１）もし、気体の分子と壁との衝突が非弾性衝突（e<1）だとすると、どうなるか。

　曖昧模糊とした質問ですが、何人か聞くと、なかなか鋭いことを見抜く生徒が必ず登場します。

　答の例：ぶつかるたびに分子が遅くなるので、気体の圧力が下がる、気体の温度が下がる、など。

　これらの現象は実際には起きませんから、分子と壁との衝突が弾性衝突であることを日常の経験から、確認することができます。

　この問のあと、衝突後の分子のx方向の速度成分、分子の運動量変化、分子が壁から受ける力積、壁が分子から受ける力積を問い、さらに一つの分子がt秒間に壁Sとぶつかる回数を問います。

　これらができれば（全員ができるわけではないので、段階的に質疑応答や答え合わせ、解説をします）これらを組み合わせて、一つの分子がt秒間に壁Sに及ぼす力積、そして、平均の力を問います。

　グラフは分子と壁による衝突（赤い面積が力積）ですが、それと同じ面積になるように平均の力×時間で四角い形を作ることで、平均の力を求めるヒントになっています。こちらは、教科書にもたいてい載っている図ですね。

パート２：箱の中のすべての分子が壁Sに及ぼす圧力を、数学の平均値の定義、物理の圧力の定義を用いて導く。

　高校の教科書ではいきなり速度vxの２乗の和をその平均値×分子数と表して説明を進めていますが、これは数学の苦手な生徒にとってはつらい。数学の平均値の定義、あるデータの平均値＝データの和／データ数、をおさらいしてから物理の内容に入ります。

　パート１で出したのは１つの分子が壁に及ぼす平均の力なので、平均といっても１つ１つの分子が壁に及ぼす力は異なりますから、気体が壁に及ぼす力を求めるには、各分子が及ぼす力の合計を求める必要があります。

　こういう背景を説明しないと、このパートのΣを使った計算は、多くの生徒にとっては、自分が何をやっているのかわからない、という状況を招きます。

　この流れに沿って設問を段階的に設定して計算させていくと、多くの生徒は自力で、合計の力を分子のx方向の速度の２乗の平均値で表すことができます。ここまでたどり着けたら、圧力の定義にしたがって、気体が壁に及ぼす圧力をvxの２乗の平均値で表すことができます。

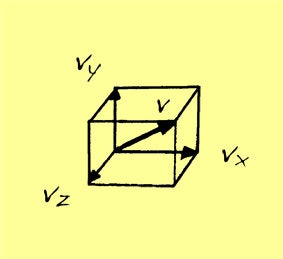
パート３：vの２乗とvxの２乗との関係を、物理的な概念と数学のベクトルの性質を用いて見つけ、気体が壁に及ぼす圧力を分子の速度の２乗の平均値で表す。

　ここが高校生のレベルを超える場面なのですが、未知に挑戦するのが自然科学の醍醐味だとすると、もっともそれが楽しめる部分になります。

　それは、分子の熱運動という乱雑な運動を、vxの２乗の平均、vyの２乗の平均、vzの２乗の平均で、いかに数式として表すか、という問です。すごく難しい問題ですね。

　でも、ぼくは自分の授業の鉄則として、こういう発見に関わる部分は、できる限り生徒に挑戦してもらうようにしています。

　もちろん、これを見抜ける生徒はごくわずかですが、挑戦する時間を設けることで、本来の自然科学の意味を体験することができます。答の出ない問題を考える時間は、決して無駄ではありません。

　大半の生徒はうーんとうなったままですが、やがていろいろな式を書き始めます。

　vxの２乗の平均+vyの２乗の平均+vzの２乗の平均=0

　うーん、残念。これだと、全部ゼロになっちゃうねえ・・・などと生徒の間を回りながら見ていくと、面白いことに、正解に辿り着く生徒が、複数出てきます。

　vxの２乗の平均=vyの２乗の平均=vzの２乗の平均

　やるなあ・・・

　できた生徒は大得意。センスあります。運動がでたらめ、ということは、方向による差がないのですから、正解者の式を示して、そういう説明をすると、みんな「なるほど」と、正解者の方をうらやましそうに見る。

　これと、ベクトルの本体と成分についてのピタゴラスの定理；

　vの２乗=vxの２乗+vyの２乗+vzの２乗

　を、平均値についても成り立つように導く問により、vxの２乗の平均=vの２乗の平均×1/3が導けます。

　クラウジウスが見つけた式（気体の圧力を気体分子の質量と個数、速度の２乗の平均値、気体の体積で表す式）が導けると、ここから先は簡単。式の変形だけなので、どの生徒もがんがん計算を進めていきます。

パート４：クラウジウスの式と状態方程式を比較することで、分子の熱運動エネルギーの平均値が絶対温度に比例することを示す。

　これは、変形のコツだけいっておけば、誰もが導けます。最後に比例定数R/NA（Rは気体定数、NAはアボガドロ数）をkB（ボルツマン定数）と書き直し（これはぼくが説明します。この授業プリントで、唯一ぼくが講義するところです）、分子運動論のプリント終了。

　・・・というところです。

　もう１枚、この続きで、分子の速度を分子量で表したり、気体の内部エネルギーを絶対温度で表すプリントがありますので、この内容を合わせて２時限分の時間をとっています。

　プリントの現物を紹介しながら説明するとよかったのですが、記事が長くなるので、今回は割愛しました。

ひろじの物理ブログ　ミオくんとなんでも科学探究隊

マンガ・イラスト＆科学の世界へようこそ。

気体の分子運動論