等加速度直線運動の公式の解釈

履修学年：高校1年もしくは高校2年

中学校で履修する方程式の文章題などで有名な「み・は・じ」の関係というものがあります。
「み」は道のり、「は」は速さ、「じ」は時間ですね。

実はこのような問題は全て「等速直線運動をしている」という前提で出題されているのです！！
具体的には、特定の区間を決まった速さで走り、その区間を走っている間は速さが変わることはないのです！！

ところが実際の物体の運動には「加速度」というものが存在して、この加速度のせいで、時間の経過に伴い速度が変わってしまい、単純な「み・は・じ」が通用しなくなってしまうのです！！

それではどうしたら、道のりを出せるのでしょうか…？

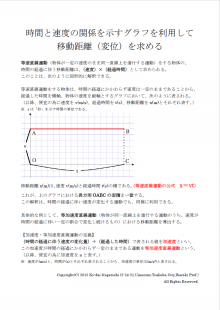
ご安心ください！！「v－tグラフ」というものが、全てを解決してくれます。

vというのは「速さ」、tというのは「時間」
このv－tグラフというのは、時間の経過に伴う速さの変化を関数のようにグラフにしたものを示すのですね。




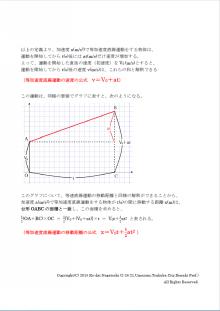
教科書で紹介されている公式の導出方法についてのみ、取り急ぎご紹介させていただきましたが、更に具体的な例につきまして、追って解説をアップロード致します。

当ブログでご紹介している問題及び単元について

・当ブログの「教科書内容の解説」は、教科書の補助を想定して執筆しているものです。従いまして、教科書で調べれば十分理解できると見られる用語の解説は割愛させていただいております。予めご了承ください。

・教科書に掲載される順序と、当ブログでご紹介いたす順序も一致しておらず、当ブログ筆者（長通幸大）の裁量に基づいております。

・Twitter問題の解答と解説は「自作問題数学bot」（https://twitter.com/mathquestionakt）という理系学部生の方のアカウントで出題されたものを主にご紹介しております。全問で問題作成者の方
から正解の確認を得ておりますので、ご参考にしていただければ幸いです。

・筆者の判断により、予告なく解説を修正したり、記事を削除したりする場合がございますが、そのことに対する読者様からの苦情は受け付けかねます旨、予めご了承ください。

二次関数の利用(時間と移動距離の関係)

「比例・反比例・一次関数・二次関数」のうち、二次関数の分野の続きです。

「一定の速さで運動する場合は、道のりが時間に比例する」ということは「比例・反比例の利用」でわずかながらご紹介致しました！！

これが斜面や空中を落下する場合はそうもいかないのです。
本題でご紹介の通り、二次関数の関係をなすのです！！




このようなことが起きる理由をちょっとだけ説明致しますね。

物理に「慣性の法則」というものがあり、この慣性の法則から、一定の速度で運動する（もしくは、運動せず静止する）ということは、その物体は運動する方向に力がはたらいていない、あるいははたらく力がつり合っていることがわかります。
なので、「水平な道を一定の速さで運動している」ということは、その物体は「運動する向きに力を受けていない」と解釈できるのですね。

ところが、運動する方向に力がはたらいている場合は、その力によって速さが変わってしまうのです！！
これは、運動方程式F＝maと表現されるもので、Fは物体が運動する向きにはたらく力の大きさ、mは物体の質量、aは物体の速度が変わるペース（物理用語で「加速度」といいます。）を示し、これが「運動する方向にはたらく力の大きさによって、速さが変わるペースが定まる」ことを説明しているのです！！

この加速度によって、二次関数の比例定数aが定まるのですが、「運動する方向にはたらく力の大きさ」の計算方法は高校物理の範囲になってしまいますので、本題では最低限のご説明に留めさせていただきますが、運動方程式「F＝ma」や「加速度が存在する運動の時間と位置の関係」につきましては、追って高校物理のテーマで解説をアップロード致します。