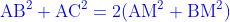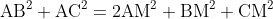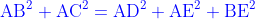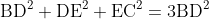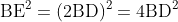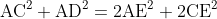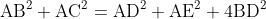中線定理の拡張？

あまりきれいではないですが，中線定理の拡張を考えたので，書いてきます．

まずは，普通の中線定理です．

定理１．（中線定理）

△ABCにおいて，辺BCの中点をMとするとき，

　　

が成り立つ．

 

とすれば，式はB,Cに関して対称です．

次に3等分バージョンです．これは問題集に載っていました．これがきっかけで「中線定理」の拡張を考えてみようと思いました．

定理２．

△ABCにおいて，辺BCを3等分する点をD,Eとするとき，

　　

が成り立つ．

定理２は，中線定理の拡張に違いないですが，

　（あ）中線定理の右辺にあった"2"はどこにいったのか．

　（い）となりそうなのに，

といったギャップがあります．

とりあえず，定理２を証明してみます．中線定理を使って証明すると次のようになります．

証明．△ABEに中線定理を用いると，

　　・・・①

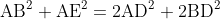
△ADCに中線定理を用いると，

　　・・・②

①＋②より

　　□

この証明の仕方のまま拡張すると，

定理３．

△ABCにおいて，辺BCをn+1等分する点をD_1,D_2,...,D_nとするとき，

　

が成り立つ．

証明．B=D_0,　C=D_{n+1}と書くことにする．D_kD_{k+1}=d　(k=0,1,...n+1)とおく．

△AD_kD_{k+2}に中線定理を用いると，

　

k=0,1, ... ,n-1の和をとると，

　

となり，定理は成り立つ．　□

右辺は，辺のｎ等分線？のうち両端のものが残る．