追記
正5角形の部分について動画を作ってみました。
黄金比φについてまとめました。
・黄金比φは、φ²=φ+1を満たす数(2つある)のうち正の方です。値は(1+√5)/2です。他方の負の数は(1-√5)/2=1-φ=-φ⁻¹です(フィボナッチ数列に登場します)。
・φの値は約1.6180であり、1:φ=5:8.0902とほぼ5:8となります。
☆黄金比の累乗とフィボナッチ数列
・φ²=φ+1やφ⁻¹=φ-1を用いて簡単にします。
・φⁿ⁺¹におけるφの係数および定数項は、
φの係数:φⁿの定数項がφⁿ⁺¹におけるφの係数になり、φⁿにおけるφの係数はφ²=φ+1より、φⁿ⁺¹におけるφの係数に加算されます。つまり、φⁿにおけるφの係数と定数項の和になります。
定数項:φⁿにおけるφの係数はφ²=φ+1より、φⁿ⁺¹における定数項になります。
・φ⁻⁽ⁿ⁺¹⁾におけるφの係数および定数項は、
φの係数:φ⁻ⁿにおける定数項はφ⁻¹=φ-1より、φ⁻⁽ⁿ⁺¹⁾におけるφの係数になります。
定数項:φ⁻ⁿにおけるφの係数はφ⁻⁽ⁿ⁺¹⁾における定数項になります。また、φⁿにおける定数項はφ⁻¹=φ-1より、φ⁻⁽ⁿ⁺¹⁾における定数項に減算されます。つまり、φ⁻⁽ⁿ⁺¹⁾における定数項は、φ⁻ⁿにおけるφの係数から定数項を引いたものになります。
以上より、係数を計算すると、フィボナッチ数列に近いものが見えてきました。
具体的には、
・φⁿにおけるφの係数はフィボナッチ数列そのものです。また、φ⁻ⁿにおけるφの係数の絶対値はフィボナッチ数列ですが、符号が交互になります。
・φⁿにおける定数項は、フィボナッチ数列の1つ前の値です。φ⁻ⁿにおける定数項の絶対値はフィボナッチ数列の1つ後の値で符号が交互になり、φの係数の符号と逆です。
φ⁻ⁿの符号が変動するので、(-1)ⁿを掛けて固定します。そうすると、φの係数が負、定数項が正になります。
φの係数がフィボナッチ数列で、定数項が前後に1つずれた値なので、定数項をいじってフィボナッチ数列にします。
フィボナッチ数列は第n+1項目から第n-1項目を引くと第n項目になります。
ところで、(-1)ⁿ×φ⁻ⁿ=(-φ)ⁿの符号は、φの係数の方が負、定数項が正で、漸化式を使うには第n+1項目の符号と第n-1項目の符号を逆にする必要があるので、(-φ)ⁿの前にマイナスを付けます。
そうすると、φⁿ-(-φ)⁻ⁿになり、
φの係数がフィボナッチ数の2倍、
定数項が第n-1項目−第n+1項目=(-1)×フィボナッチ数
となります。
φ=(1+√5)/2より、2φ=1+√5です。定数項のフィボナッチ数の係数が-1なので、
φⁿ-(-φ)⁻ⁿはフィボナッチ数の√5倍になります。よって√5で割るとフィボナッチ数列の一般項が求められました。
☆正五角形の中の黄金比
以下、正五角形の辺の長さを1とします。
・正五角形の対角線は5本あり、全て同じ長さです。その長さは辺の長さのφ倍です。これを導くには、相似を使う方法が一般的ですが、トレミーの定理を使うと簡単にできます(定理自体の導出が難しいですが…)。
・頂角が36°、底角が72°の尖った二等辺三角形は、底辺:斜辺=1:φになります。
これの斜辺と底辺の比からsin18°=(1/2)÷φと求められ、ここから他の三角比を導いていけます。
・頂角が72°、底角が54°の二等辺三角形は、底辺:斜辺=1:Rになります。正三角形より少し平たいです。
これの斜辺が外接円の半径R、高さが内接円の半径rなので、三角比を用いてこれらの半径が求められます。また、正五角形の面積もこれの5つ分で求められます。
・頂角が108°、底角が36°の平たい二等辺三角形は、底辺:斜辺=φ:1になります。
・頂角が144°、底角が18°のさらに平たい二等辺三角形は底辺:斜辺=φ:Rになります。
・内接円の半径rは底角が54°、底辺が1の二等辺三角形の高さなので、
r=(1/2)×tan54°=(√5/10)×√(3+4φ)~0.6882です。
・外接円の半径Rは底角が54°、底辺が1の二等辺三角形の斜辺なので、
R=(1/2)×sec54°=(√5/5)×√(2+φ)~0.8507です。
・R²=r²+(1/2)²およびφ²=(R+r)²+(1/2)²は三平方の定理から導けます。
特に後者からR+r=(1/2)×√(3+4φ)~1.5388が導かれます。
この値はRとrの値をそのまま足すより簡単に導けます(2つの根号を纏める方法は2乗したものの平方根として扱うと出来ますが、√5=2φ-1を使わないと綺麗にならないので注意しましょう)。
sec÷tan=sinなので、r=Rsin54°=φR/2となります。
Rとrの積Rr=(1+3φ)/10~0.5854も載せておきました。
・正五角形の面積は底辺が1、高さがrの二等辺三角形の5つ分なので、
(√5/4)×√(3+4φ)〜1.7205
になります。
・正五角形に外接する正10角形の辺の長さaは、底角が18°、底辺が1の二等辺三角形の斜辺なので、
a=(1/2)×sec18°=(√5/5)×√(3-φ)~0.5257です。
・正10角形の辺と中心を結んだ二等辺三角形は、頂角が36°、底辺がa、斜辺がRなので、a:R=1:φです。
R²+a²=1は計算すると出てきますが、幾何的な導出はわかりません。正五角錐の高さがaと等しくなる理由です。
三平方の定理からa²=(R-r)²+(1/2)²が導かれ、R-r=(√5/10)×√(7-4φ)~0.1625と求められます。
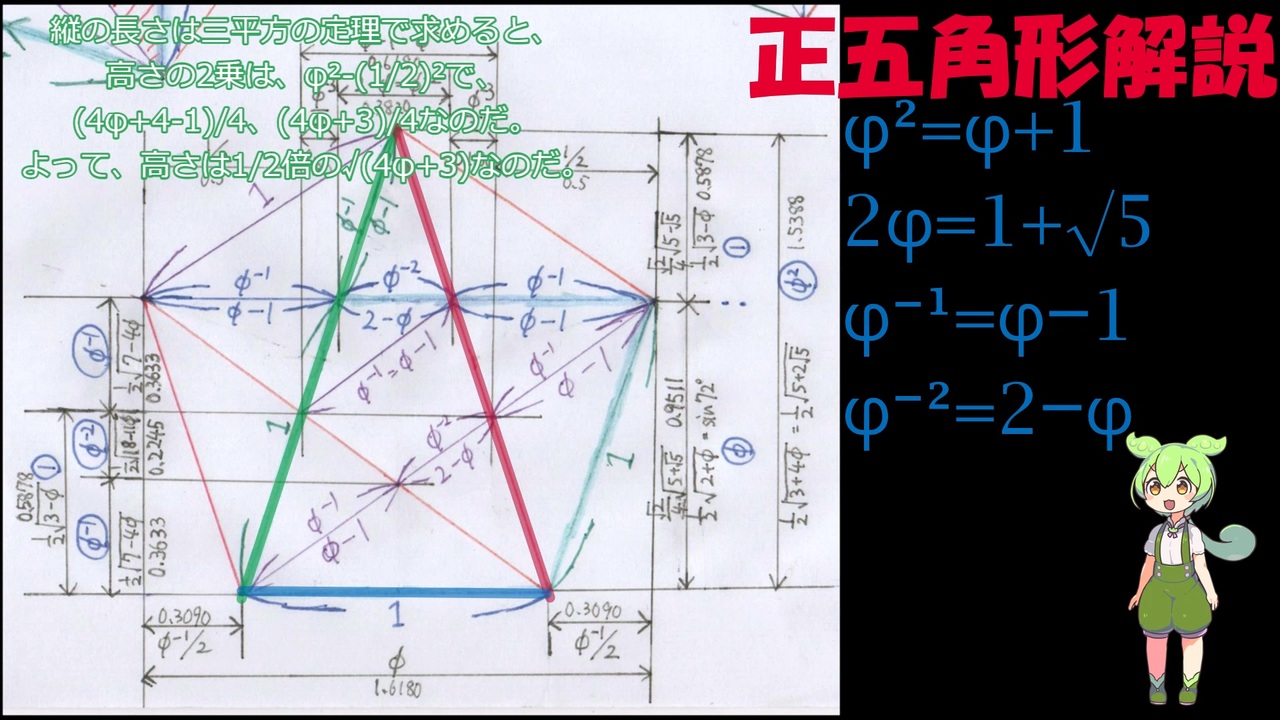
☆図の左右に各部分の高さについて付け加えました。
・底辺とそれに平行な対角線との距離は、正五角形の外角が72°なので、1×sin72°=(1/2)×√(2+φ)~0.9511です。
この距離は後述の正20面体の外接球の半径R'と等しいので、この値をR'と表記します。
・底辺から外接円までの高さは、中心からの距離の差に注目すると、R-r=(√5/10)×√(7-4φ)~0.1625と書けます。
・中心から底辺までの距離は、内接円の半径r=(√5/10)×√(3+4φ)~0.6882です。
・中心から対角線の距離は、底辺とそれに平行な対角線との距離R'から中心から底辺までの距離rを引いた長さなので、
R'-r=(√5/10)×√(3-φ)~0.2629となります。
・正五角形の高さは、外接円の半径Rと内接円の半径rの和R+r=(1/2)×√(3+4φ)~1.5388です。
・正五角形の頂点から対角線までの距離は、正五角形の高さR+rから底辺とそれに平行な対角線との距離R'を引いた距離、
R+r-R'=(1/2)×√(3-φ)~0.5878となります。
☆18°、36°、54°、72°の三角比
・18°の倍数の角の三角比には二重根号が出てきて表記や計算が面倒です。ここで黄金比φを用いると二重根号を出さずに計算できます。欠点としては、実際の値がわかりにくいところです(36°違いの三角比は符号が異なるだけだが、それが見辛くなる)。
・分母の有理化で用いる等式として、
(2+φ)×(3-φ)=5、{(5+√5)/2}×{(5-√5)/2}=5
φ×(φ-1)=1、{(1+√5)/2}×{(-1+√5)/2}=1
があります。
・先述の通り、sin18°が1/(2φ)が幾何的に簡単に求められます。次にcos36°が1-2sin²18°から、またsin²θ+cos²θ=1より、cos18°が求められます。
これらの値から他の値を求めていくと表が埋まります。
☆正20面体と黄金比
正20面体の図としてよく見かけるのが、対角線と垂直な方向から少しずらして見たものです。
ここでは、対角線の方向から見た図(上から見た図)とそれと垂直な方向から見た図(前から見た図)を使って説明していこうと思います。
・上から見た図では黒と橙で互いに逆向きな正五角形および頂点と中心を結んだ線が、青で正10角形が描かれています。何れの色の線も10本引かれているので、正20面体の辺の数は30本です。
・上側が橙の線で、下側が黒の線です。黒の線は下側なので隠れて見えません。
・前から見た図では、上からの図で正五角形だったところが直線に潰れます。
・橙と黒の部分はそれぞれ上向き、下向きの正五角錐で二等辺三角形に見えます。
・青の部分は側面の10面です。真ん中の三角形は正三角形を見えますが、実際は手前に傾いているので正三角形より少し平たいです。
・図の幅は上から見た図より、正五角形の対角線の長さなのでφです。
また、2番目と4番目の点の間は正五角形の辺の長さなので1です。
・正五角錐の高さhは正20面体の辺が斜辺で正五角形の外接円の半径Rが底辺の直角三角形の高さなので、
h=√(1-R²)=a=(√5/5)×√(3-φ)~0.5257です。
・青の部分の高さHについては、
まず、正三角形の高さが1×sin60°=√3/2です。
正三角形が斜めに傾いている量が正五角形の外接円の半径Rと内接円の半径rの差R-r=(√5/10)×√(7-4φ)です。
よって、H=√{(√3/2)²-(R-r)²}
=√{(3/4)-(1/20)×(7-4φ)}
=(√5/10)×√{15-(7-4φ)}
=(√5/10)×√{8+4φ}
=(√5/5)×√{2+φ}
=R~0.8507
と正五角形の外接円の半径Rと同じになりました。
なお、正三角形の高さは√3/2~0.8660なので、傾いたぶん少し低くなっています。
・正20面体の外接球の半径R'は正20面体の高さの半分なので、
R'=(2h+H)/2
=(√5/5)×√(3-φ)+(√5/10)×√(2+φ)
=(√5/10)×{2√(3-φ)+√(2+φ)}
=(√5/10)×√{4(3-φ)+4√{(3-φ)(2+φ)}+(2+φ)}
=(√5/10)×√{12-4φ+4√5+2+φ}
=(√5/10)×√{14-3φ+4√5}
=(√5/10)×√{10+8φ-3φ}
={√(2+φ)}/2~0.9511
と求められます。辺より少し短いです。
※正20面体の頂点は同一球面上にあるので、外接球の直径となる真裏にある2点と他の1点で出来る三角形は直角三角形になります。
直角を挟む2辺は、正20面体の1辺と正五角形の対角線φなので、直径2R'は三平方の定理より、(2R')²=1²+φ²から簡単に求められます。
・正20面体の内接球の半径r'は、斜辺が外接球の半径R'、底辺が正三角形の中心から頂点までの距離(1/√3)の直角三角形の高さだから、
r'=√{R'²-(1/√3)²}
=√{(2+φ)/4-(1/3)}
=√{(6+3φ-4)/12}
=√(φ⁴/12)
= (√3/6)×φ²
=(√3/6)×(φ+1)~0.7558
と求まりました。
・正20面体の体積Vは中心と正三角形で出来る三角錐20個ぶんで、正三角形の面積が(1/2)×1²×sin60°=√3/4なので、
V=20×(1/3)×(√3/4)×r'
=(5/6)×(φ+1)~2.1817
と求められました。
・正五角錐の体積V₁は、高さが(√5/5)×√(3-φ)、底面の正五角形の面積が(√5/4)×√(3+4φ)なので、
V₁=(1/3)×(√5/5)×√(3-φ)×(√5/4)×√(3+4φ)
=(1/12)×√{(3-φ)(3+4φ)}
=(1/12)×√(-4φ²+9φ+9)
=(1/12)×√(5φ+5)
=(√5/12)×φ
√5=2φ-1を用いるとさらに綺麗に表記できます。
=(φ+2)/12~0.3015
と求まりました。
・青の部分(捻じれた正五角柱、正反五角柱という)の体積をV₂とすると、
V=V₂+2V₁、V=(5/6)×(φ+1)、V₁=(φ+2)/12より、
V₂=V-2V₁=(5/6)×(φ+1)-(φ+2)/6
={5(φ+1)-(φ+2)}/6
=(4φ+3)/6
と求まりました。