調和級数の部分和(過去の記事:https://ameblo.jp/mossalmon/entry-12320091570.html)を求める際にはオイラーの定数というものが出現します。
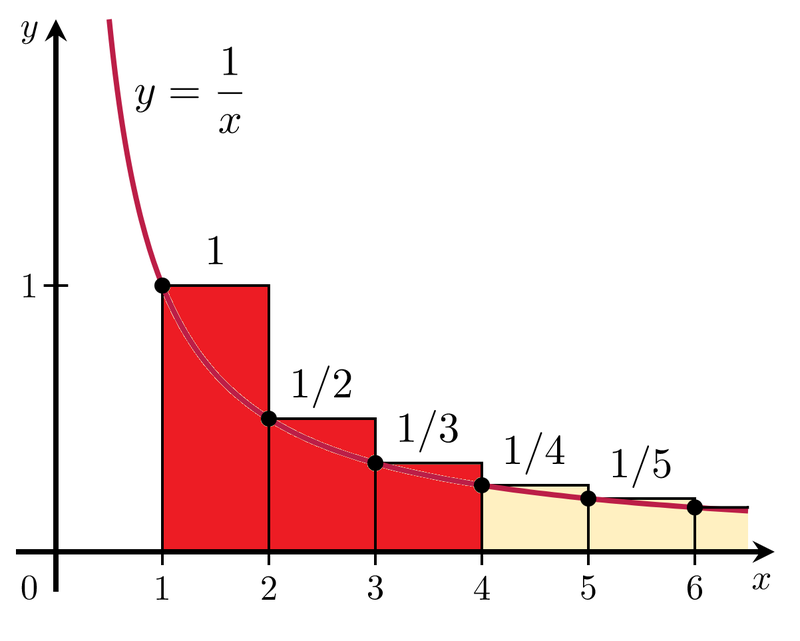
ここで、オイラー定数の図形的意味を考えてみると、
例えばn=3の時を考えてみると、
γは階段状の部分から1/xの面積を引いた残りの部分のことなので、
γはしたのピンクの部分の面積の総和になります。
ε_k はn≧4における緑の部分の総和の絶対値です。γで足しすぎた半月の分を引きます。nが無限大になると引く必要はないのでε_kは0です。
ここで、以下のような数列を定義すると、
γはn→∞のときの極限値です。
γが収束することを証明するには、
・a_nが単調に減少すること
・a_nが下に有界であること
を証明すればよいわけです。
証明については下のurlの内容を参照してください。
結果としてγは収束して
が得られますが、γの計算は非常に厄介で、γが有理数か無理数化さえわかっていません。
「調和級数の発散とオイラー定数」受験の月
http://examist.jp/mathematics/integration-expression/euler-teisu/