1から100までの数字をすべて足すといくらになるか？という問いは有名な問題であり、小学生の時に1回は聞かれるものです。式を反対にして(100+99+…+1)足し合わせ、2で割って5050を得ることができます。
では、
この式を瞬時に計算することはできるでしょうか？上の問題のような計算はうまくいかず、簡単には計算できません。この計算を一般化してみます。
ここで、級数 
は調和級数と呼ばれるもので、上の式はそのnまでの部分和ということができます。調べたところ、驚くべきことにこの部分和の初等関数による表示は現在も確立されていないようです。初等関数による表示が不可能なのか、まだ計算されていないだけなのかはわかりません。
今回は、この調和級数の部分和について近似式を作ることができたので、紹介します。
まず、調和級数はグラフでは y=1/x に覆いかぶさるような形で存在しています。
そこで、下のグラフのようにy=1/xの部分(赤色）は積分で面積を求め、さらに上の三角形(青色）の部分を足し合わせて計算します。
まず、赤色の部分はy=1/x を1からn+1まで積分したものであるので、面積をs_1とすると、
次に、青色の部分の面積をs_2とすると、s_2は底辺が1、高さが合計 1-(1/(n+1))の三角形の面積の総和であり、
であるから、
となります。
つまり、調和級数の部分和の近似式として
が得られるわけです。
ここで、赤色と青色に挟まれた部分が真の値との誤差になってきます。この部分をどう処理するかは考え中です。
出来上がった近似式をもとにn=1から100まで計算してグラフにしてみました。グラフを見てみると、近似式によるグラフは調和級数とほぼ同様な形・値をとっていることが分かります。
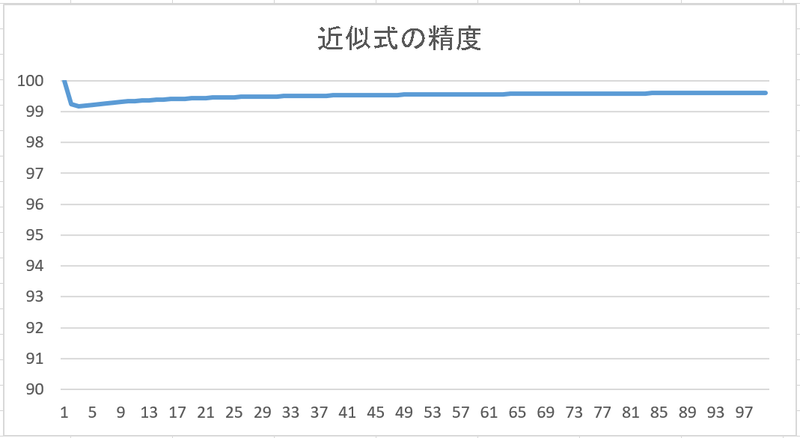
さらに、(真の値)/(近似値)から、近似式の精度を計測してみます。
n=1のときのみ94.3%ですが、n=2になると95.5%となり、その後は精度が上がってやがて98%以上になります。
非常に単純な計算ではありますが、精度が95%を超えるので、近似としては悪くないのではないかと思います。
得られた近似式の持っているメリットとしては、
・初等関数による比較的簡単な式として表現できる
・連続関数として扱える
・滑らかな関数として扱える
などがあげられます。
ただ、グラフで計算に加えることができなかった部分（赤色と青色に挟まれた部分）について、
・この部分を三角形などで近似して計算に加えられないか？
・面積の和は収束するのか？（＝誤差は一定となるか？）
については課題があります。
一方で、調和級数の表現として、
というものがあります。ここで、γはオイラーの定数というもので、調和級数から1/xのグラフの1から∞までの面積をひいたものであり、
としてあらわされます。この値は収束して
という値になるようです。
ちなみに、この定数はガンマ関数との関連もあり、
の対数微分にz=1を代入して
とすることもできるようです。
さらに、ε_k はk→∞で0になる値で、変動するものですが微小な値です。
今回得られた近似式における
は、オイラーの定数のような役割を担っていると考えています。
最初の質問に戻り、n=100のときの調和級数の部分和について、近似式によると
から、結果は約5,11であり、真の値
にたいして98.51%の精度で近似値を求めることができました。
追記：
誤差はn=1のときの半月型の部分を足してやることで大幅に解消されます。
このグラフのn=1において存在する半月型の部分です。以下「半月」と呼びます
半月の面積は3/4-log2なので、
このような形で定数を補ってあげると、式がやや煩雑にはなりますが、精度が上がります。
上のグラフのように、最も精度が落ちるn=3でも精度は99％を超えました(99.172%)。
99%から100%を拡大した詳しいグラフです。nが小さいほど誤差が大きいのが弱点なので、半月一個分を補ってやるだけで大幅に誤差が解消されます。
定数項を計算していくことで、さらに精度を上げていくことも可能になります。必要に応じて精度を変えていける点も魅力的です。
ただ、この半月の部分の面積の総和は一般化することが現状不可能であり（一般化できたら調和級数の部分和そのものが一般化できる）、手計算なりコンピュータなりを駆使して地道に求めていくしかないようです。
また、半月の面積の総和とn/2(n+1)の極限の合計はオイラーの定数に収束します。なので、先に誤差の集合体である(オイラーの定数 -1/2)を足すとよいのではないのではないかという話になります。
近似式にオイラーの定数を足して精度を計測してみます。
精度が大幅に上昇しました。もっとも悪いn=1のときで97.9637%、n=2では99.3893%となり、n=100でなんと99.99984%となります。これは非常に実用的なのではないでしょうか？
結論を示します。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
調和級数のnまでの部分和について、以下の近似式が成立する。
ただし、γはオイラーの定数0.57…である
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
注記：
この文章で用いた「精度」は、100*(1-相対誤差)によって計算しています。相対誤差は、|近似値-真の値|/真の値です。
参考HP :
「調和級数」 wikipedia
https://ja.wikipedia.org/wiki/%E8%AA%BF%E5%92%8C%E7%B4%9A%E6%95%B0
「オイラーの定数」 wikipedia
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E3%81%AE%E5%AE%9A%E6%95%B0
「調和級数1+1/2+1/3…が発散することの証明」 高校数学の美しい物語 https://mathtrain.jp/tyowa
「調和級数の部分和の式はないんですか」
yahoo!Japan 知恵袋 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11103253006
「相対誤差の計算方法と意義」具体例で学ぶ数学
https://mathwords.net/soutaigosa