Işık Gerçekten Nedir?

Gözlerinizi kapatın ve bir ormanın içinde olduğunuzu hayal edin. Ardından güneşten yola çıktıktan 8 dakika sonra yeryüzüne ulaşacak bir ışık hüzmesini hayal edin. Işık, yapraktan yansıyıp gözlerimizdeki alıcıları harekete geçirdiğinde beynimizin yaprağın rengini “yeşil” olarak algıladığını hepimiz biliyoruz. Ancak gerçekten ışığın doğası neydi?

17. yüzyılda, İngiliz bilim insanı Isaac Newton ışığın sıcak cisimlerden yayılan çok küçük parçacıklar olduğunu düşünürken, yine aynı yüzyılda Hollandalı bilim insanı Huygens, ışığın her yöne doğru titreşen bir dalga olduğunu düşünmüştü. Ancak iki bilim insanı da ışığın tam olarak doğasını açıklayamamışlardı.

19. yüzyılda Danimarkalı bilim insanı Orsted, elektrik ile ilgili verdiği bir konferansta bataryayı açıp kapama sırasında yanında bulunan kumpasın iğnesinin ani hızlanmasını göstermişti. Bu deney, elektrik alanda meydana gelen değişimin manyetik alan oluşturduğunu ve bu durumda elektrik ile manyetizmanın birbiri arasında ilişkili olduğunu gösteriyordu. Ünlü bilim insanı Faraday ise, 11 yıl sonra bu durumun tersini yani manyetik alandaki değişimin, elektrik alanı oluşturduğunu keşfetti.

İskoç bilim insanı Maxwell, bu iki durumu tek çatı altında elektromanyetizma teoreminde birleştirdi ve yaptığı çalışmalarında elektrik alandaki değişmenin manyetik alan oluşturduğunu, oluşan manyetik alanın tekrar elektrik alanı tetiklediğini ve bu durumun çok çok hızlı bir şekilde uzayda hareket ederek sonsuz tekrara girdiğini saptadı. Bu aşırı hızlı hareketin uzayda yaklaşık 300,000,000 m/s hızla seyahat ettiğini hesapladı ve bu değer bildiğimiz ışık hızı değerine oldukça yakındı. ^[1]

Ve tüm bu bilimsel ispatlardan, ışığın gerçek tanımının; “elektrik ve manyetik alanın birbirinden ayrılmayacak şekilde uzayda hareket etmesi” olduğunu söyleyebiliriz.

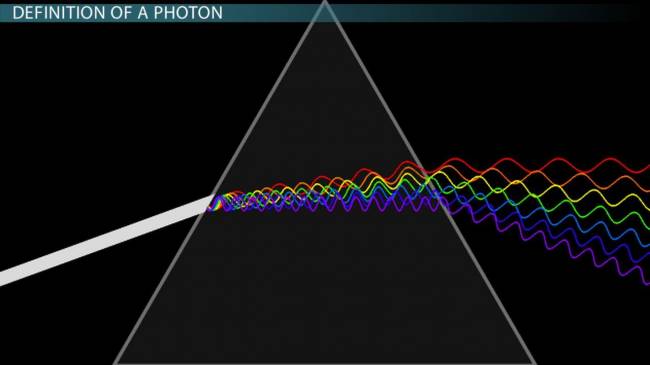
Işığın Renklere Ayrılması ve Uzaydaki Hareketi

Daha iyi algılayabilmek adına, elektrik alan ile manyetik alanı birer dansçı olarak düşünürsek, her birinin, içerisinde manyetik ve elektrik alana ait parçaları barındırarak (örneğin, ışığın temel birimi olan fotonlar), birbirine sıkıca tutunup, uzayda dans ederek seyahat ettiklerini düşünebiliriz.

Her elektromanyetik dalga, bir dalga boyu (dansçıların bir adımlarının uzunluğu olarak düşünülebilir) değerine sahiptir. Yüksek enerjiye sahip gama ışınlarının dalga boyu hidrojen atomundan bile küçükken, düşük enerjili radyo dalgalarının ise Jüpiter’in genişliği kadar olabilir. ^[2]

Görünür ışık bölgesindeki ışıkların dalga boyları, insan saçının kalınlığının %1’i kadarına denk gelmekte ve elektromanyetik spektrumda bu çok küçük bir kısıma tekabül etmektedir. Biz sadece 400 ila 700 nanometre değerleri arasındaki dalga boyuna sahip ışıkları görebilmekteyiz. ^[2]

Görme uzvumuzun çalışma prensibi bir çeşit kimyasal reaksiyondan ibaret ve bu reaksiyonun başlaması için gereken tek şey ise sadece “ışık”. Işığın bu reaksiyonu başlatıp, beynimize sinyal gönderip renkleri ve çevreyi algılayabilmemiz için belirli dalga boyuna sahip olması gerekmektedir.

Dalga boyu eğer büyük olursa, kimyasal reaksiyonu tetikleyemez ve bu yüzden büyük dalga boylarını insanlar algılayamaz. Eğer dalga boyu küçük olursa, çok fazla enerji taşıdıklarından, reaksiyona girecek hücrelere hasar verir ve görme uzuvlarımız zarar görür. Aynı şekilde küçük dalga boyuna sahip ışınların bu etkisi, ultraviyole ışınlarının cildimizde güneş yanıkları oluşturmasının nedeni olarak da açıklanabilir. Bunun yanında, görünür ışık bölgesi içinde yer alan ışınlar, su içerisinde absorbe olmadan uzun mesafe kat edebilirler ve bu nedenle gözlerimiz suyu saydam olarak algılar.

Tekrar ormana geri dönelim ve ağacın yaprağına tekrar bakalım. Güneşten gelen elektrik ve manyetik alanın oluşturduğu dalga, yapraktan yansıyarak retinamıza çarpar ve gözümüzde kimyasal reaksiyon oluşumunu tetikleyerek beynimize giden sinyali oluşturup, yaprağın rengini “yeşil” olarak algılamamızı sağlar.

Görsel Kaynak
http://embed.wistia.com/deliveries/73f3dc561af2b4c535df1d30c2c7e1cb0b6a3910.jpg

Kapak Görseli
http://www.kisa.link/5JXy

Kaynaklar
[1] https://www.newscientist.com/article/mg13217934-200-what-is-light/
[2] https://lco.global/spacebook/what-is-light/

https://www.fizikist.com/isik-gercekten-nedir/

興味深く読みました：

再生核研究所声明314（2016.08.08）　世界観を大きく変えた、ニュートンとダーウィンについて

今朝２０１６年８月６日，散歩中　目が眩むような大きな構想が閃いたのであるが、流石に直接表現とはいかず、先ずは世界史上の大きな事件を回想して、準備したい。紀元前の大きな事件についても触れたいが当分　保留したい。

そもそも、ニュートン、ダーウィンの時代とは　中世の名残を多く残し、宗教の存在は世界観そのものの基礎に有ったと言える。それで、アリストテレスの世界観や聖書に反して　天動説に対して地動説を唱えるには　それこそ命を掛けなければ主張できないような時代背景が　存在していた。

そのような時に世の運動、地上も、天空も、万有を支配する法則が存在するとの考えは　それこそ、世界観の大きな変更であり、人類に与えた影響は計り知れない。進化論　人類も動物や生物の進化によるものであるとの考えは、　人間そのものの考え方、捉え方の基本的な変更であり、運動法則とともに科学的な思考、捉え方が世界観を根本的に変えてきたと考えられる。勿論、自然科学などの基礎として果たしている役割の大きさを考えると、驚嘆すべきことである。

人生とは何か、人間とは何か、―　世の中には秩序と法則があり、人間は作られた存在で

その上に　存在している。如何に行くべきか、在るべきかの基本は　その法則と作られた存在の元、原理を探し、それに従わざるを得ないとなるだろう。しかしながら、狭く捉えて　唯物史観などの思想も生んだが、それらは、心の問題、生命の神秘的な面を過小評価しておかしな世相も一時は蔓延ったが、自然消滅に向かっているように見える。

自然科学も生物学も目も眩むほどに発展してきている。しかしながら、人類未だ成長していないように感じられるのは、止むことのない抗争、紛争、戦争、医学などの驚異的な発展にも関わらず、人間存在についての掘り下げた発展と進化はどれほどかと考えさせられ、昔の人の方が余程人間らしい人間だったと思われることは　多いのではないだろうか。

上記二人の巨人の役割を、自然科学の基礎に大きな影響を与えた人と捉えれば、我々は一段と深く、巨人の拓いた世界を深めるべきではないだろうか。社会科学や人文社会、人生観や世界観にさらに深い影響を与えると、与えられると考える。

ニュートンの作用、反作用の運動法則などは、人間社会でも、人間の精神、心の世界でも成り立つ原理であり、公正の原則の基礎（再生核研究所声明 1　(2007/1/27)：　美しい社会はどうしたら、できるか、美しい社会とは）にもなる。　自国の安全を願って軍備を強化すれば相手国がより、軍備を強化するのは道理、法則のようなものである。慣性の法則、急には何事でも変えられない、移行処置や時間的な猶予が必要なのも法則のようなものである。力の法則　変化には情熱、エネルギー，力が必要であり、変化は人間の本質的な要求である。それらはみな、社会や心の世界でも成り立つ原理であり、掘り下げて学ぶべきことが多い。ダーウィンの進化論については、人間はどのように作られ、どのような進化を目指しているのかと追求すべきであり、人間とは何者かと絶えず問うて行くべきである。根本を見失い、個別の結果の追求に明け暮れているのが、現在における科学の現状と言えるのではないだろうか。単に盲目的に夢中で進んでいる蟻の大群のような生態である。広い視点で見れば、経済の成長、成長と叫んでいるが、地球規模で生態系を環境の面から見れば、癌細胞の増殖のような様ではないだろうか。人間の心の喪失、哲学的精神の欠落している時代であると言える。

以　上

再生核研究所声明315（2016.08.08）　世界観を大きく変えた、ユークリッドと幾何学

ニュートン、ダーウィンの大きな影響を纏めたので（声明３１４）今回はユークリッド幾何学の影響について触れたい。

ユークリッド幾何学の建設について、ユークリッド自身（アレクサンドリアのエウクレイデス（古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid（ユークリッド）、紀元前3世紀? - ）は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』（ユークリッド原論）の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下（紀元前323年-283年）のアレクサンドリアで活動した。）が絶対的な幾何学の建設に努力した様は、『新しい幾何学の発見―ガウスボヤイロバチェフスキー』リワノワ著松野武訳1961　東京図書　に見事に描かれており、ここでの考えはその著書に負うところが大きい。

ユークリッドは絶対的な幾何学を建設するためには、絶対的に正しい基礎、公準、公理に基づき、厳格な論理によって如何なる隙や曖昧さを残さず、打ち立てられなければならないとして、来る日も来る日も、アレクサンドリアの海岸を散歩しながら　ユークリッド幾何学を建設した（『原論』は19世紀末から20世紀初頭まで数学（特に幾何学）の教科書として使われ続けた[1][2][3]。線の定義について、「線は幅のない長さである」、「線の端は点である」など述べられている。基本的にその中で今日ユークリッド幾何学と呼ばれている体系が少数の公理系から構築されている。エウクレイデスは他に光学、透視図法、円錐曲線論、球面天文学、誤謬推理論、図形分割論、天秤などについても著述を残したとされている。）。

ユークリッド幾何学、原論は２０００年以上も越えて多くの人に学ばれ、あらゆる論理的な学術書の記述の模範、範として、現在でもその精神は少しも変わっていない、人類の超古典である。―　少し、厳密に述べると、ユークリッド幾何学の基礎、いわゆる第５公準、いわゆる平行線の公理は徹底的に検討され、２０００年を経て公理系の考えについての考えは改められ―　公理系とは絶対的な真理という概念ではなく、矛盾のない仮定系である　―　、非ユークリッド幾何学が出現した。論理的な厳密性も徹底的に検討がなされ、ヒルベルトによってユークリッド幾何学は再構成されることになった。非ユークリッド幾何学の出現過程についても上記の著書に詳しい。

しかしながら、ユークリッド幾何学の実態は少しも変わらず、世に絶対的なものがあるとすれば、それは数学くらいではないだろうかと人類は考えているのではないだろうか。

数学の不可思議さに想いを致したい（しかしながら、数学について、そもそも数学とは何だろうかと問い、ユニバースと数学の関係に思いを致すのは大事ではないだろうか。この本質論については幸運にも相当に力を入れて書いたものがある：

No.81, May 2012(pdf 432kb)

19/03/2012

ここでは、数学とは何かについて考えながら、数学と人間に絡む問題などについて、幅.広く面白く触れたい。

）。

―　数学は公理系によって定まり、そこから、論理的に導かれる関係の全体が一つの数学の様にみえる。いま予想されている関係は、そもそも人間には無関係に確定しているようにみえる。その数学の全体はすべて人間には無関係に存在して、確定しているようにみえる。すなわち、われわれが捉えた数学は、人間の要求や好みで発見された部分で、その全貌は分からない。抽象的な関係の世界、それはものにも、時間にも、エネルギーにも無関係で、存在している。それではどうして、存在して、数学は美しいと感動させるのであろうか。現代物理学は宇宙全体の存在した時を述べているが、それでは数学はどうして存在しているのであろうか。宇宙と数学は何か関係が有るのだろうか。不思議で不思議で仕方がない。数学は絶対で、不変の様にみえる。時間にも無関係であるようにみえる。数学と人間の関係は何だろうか。―

数学によって、神の存在を予感する者は　世に多いのではないだろうか。

以　上

再生核研究所声明368（2017.5.19）ゼロ除算の意義、本質

ゼロ除算の本質、意義について、既に述べているが、参照すると良くまとめられているので、初めに復習して、新しい視点を入れたい。

再生核研究所声明359（2017.3.20）　ゼロ除算とは何か　―　本質、意義

ゼロ除算の理解を進めるために　ゼロ除算とは何か　の題名で、簡潔に表現して置きたい。　構想と情念、想いが湧いてきたためである。

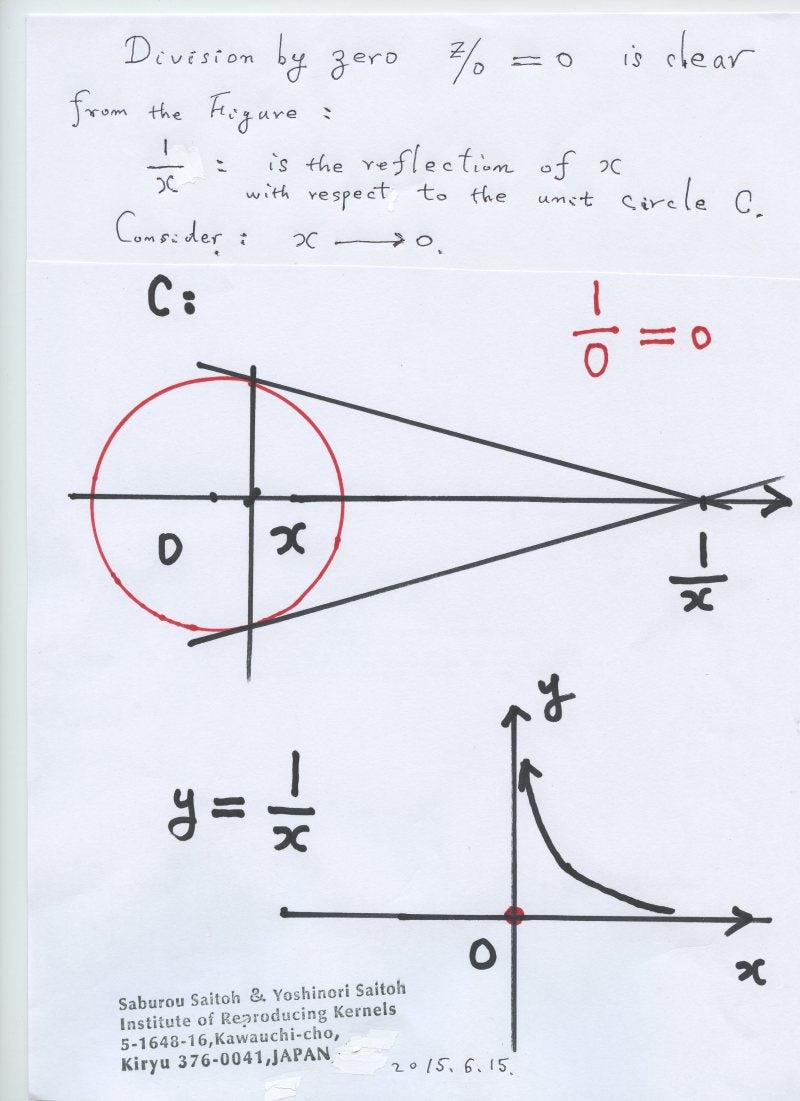
基本的な関数y=1/x を考える。　これは直角双曲線関数で、原点以外は勿論、値、関数が定義されている。問題はこの関数が、x=0 　で　どうなっているかである。結論は、この関数の原点での値を　ゼロと定義する　ということである。　定義するのである。定義であるから勝手であり、従来の定義や理論に反しない限り、定義は勝手であると言える。原点での値を明確に定義した理論はないから、この定義は良いと考えられる。それを、y=1/0=0　と記述する。ゼロ除算は不可能であるという、数学の永い定説に従って、1/0　の表記は学術書、教科書にもないから、1/0=0　の記法は　形式不変の原理、原則　にも反しないと言える。―　多くの数学者は注意深いから、1/0=\infty　の表記を避けてきたが、想像上では x　が　0　に近づいたとき、限りなく　絶対値が大きくなるので、複素解析学では、表現1/0=\infty　は避けても、1/0=\infty　と考えている事は多い。（無限大の記号がない時代、アーベルなどもそのような記号を用いていて、オイラーは1/0=\inftyと述べ、それは間違いであると指摘されてきた。　しかしながら、無限大とは何か、数かとの疑問は　続いている。）。ここが大事な論点である。近づいていった極限値がそこでの値であろうと考えるのは、極めて自然な発想であるが、現代では、不連続性の概念　が十分確立されていて、極限値がそこでの値と違う例は、既にありふれている。―　アリストテレスは　連続性の世界観をもち、特にアリストテレスの影響を深く受けている欧米の方は、この強力な不連続性を中々受け入れられないようである。無限にいくと考えられてきたのが突然、ゼロになるという定義になるからである。　しかしながら、関数y=1/xのグラフを書いて見れば、原点は双曲線のグラフの中心の点であり、美しい点で、この定義は魅力的に見えてくるだろう。

定義したことには、それに至るいろいろな考察、経過、動機、理由がある。―　分数、割り算の意味、意義、一意性問題、代数的な意味づけなどであるが、それらは既に数学的に確立しているので、ここでは触れない。

すると、定義したからには、それがどのような意味が存在して、世の中に、数学にどのような影響があるかが、問題になる。これについて、現在、初等数学の学部レベルの数学をゼロ除算の定義に従って、眺めると、ゼロ除算、すなわち、　分母がゼロになる場合が表現上現れる広範な場合に新しい現象が発見され、ゼロ除算が関係する広範な場合に大きな影響が出て、数学は美しく統一的に補充，完全化されることが分かった。それらは現在、３８０件以上のメモにまとめられている。しかしながら、世界観の変更は特に重要であると考えられる：

複素解析学で無限遠点は　その意味で1/0=0で、複素数0で表されること、アリストテレスの連続性の概念に反し、ユークリッド空間とも異なる新しい空間が　現れている。直線のコンパクト化の理想点は原点で、全ての直線が原点を含むと、超古典的な結果に反する。更に、ゼロと無限の関係が明らかにされてきた。

ゼロ除算は、現代数学の初等部分の相当な変革を要求していると考えられる。

以　上

ゼロ除算の代数的な意義は、山田体の概念で体にゼロ除算を含む構造の入れ方、一般に体にゼロ除算の概念が入れられるが、代数的な発展については　専門外で、触れられない。ただ、計算機科学でゼロ除算と代数的な構造について相当議論している研究者がいる。

ゼロ除算の解析学的な意義は、従来孤立特異点での研究とは、孤立点での近傍での研究であり、正確に述べれば　孤立特異点そのものでの研究はなされていないと考えられる。

なぜならば、特異点では、ゼロ分のとなり、分子がゼロの場合には　ロピタルの定理や微分法の概念で　極限値で考えてきたが、ゼロ除算は、一般に分子がゼロでない場合にも意味を与え、極限値でなくて、特異点で　何時でも有限確定値を指定できる　―　ゼロ除算算法。初めて、特異点そのものの世界に立ち入ったと言える。従来は孤立特異点を除いた世界で　数学を考えてきたと言える。その意味でゼロ除算は　全く新しい数学、世界であると言える。典型的な結果は tan(\pi/2) =0で、y軸の勾配がゼロであることである。

ゼロ除算の幾何学的な意義は、ユークリッド空間のアレクサンドロフの1点コンパクト化に、アリストテレスの連続性の概念でない、強力な不連続性が現れたことで、全く新しい空間の構造が現れ、幾何学の無限遠点に関係する部分に全く新規な世界が現れたことである。所謂無限遠点が数値ゼロで、表現される。

さらに、およそ無限量と考えられたものが、実は、数値ゼロで表現されるという新しい現象が発見された。tan(\pi/2) =0の意味を幾何学的に考えると、そのことを表している。これはいろいろな恒等式に新しい要素を、性質を顕にしている。ゼロが、不可能性を表現したり、基準を表すなど、ゼロの意義についても新しい概念が現れている。

以　上

ゼロ除算の詳しい解説を次で行っている：

（数学基礎学力研究会のホームページ

URLは

http://www.mirun.sctv.jp/~suugaku

http://okmr.yamatoblog.net/

）

The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world

Division by Zero z/0 = 0 in Euclidean Spaces

Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh

International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1

-16.　

http://www.scirp.org/journal/alamt　　http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf

http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi

http://okmr.yamatoblog.net/

Relations of 0 and infinity

Hiroshi Okumura, Saburou Saitoh　and Tsutomu Matsuura：
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…