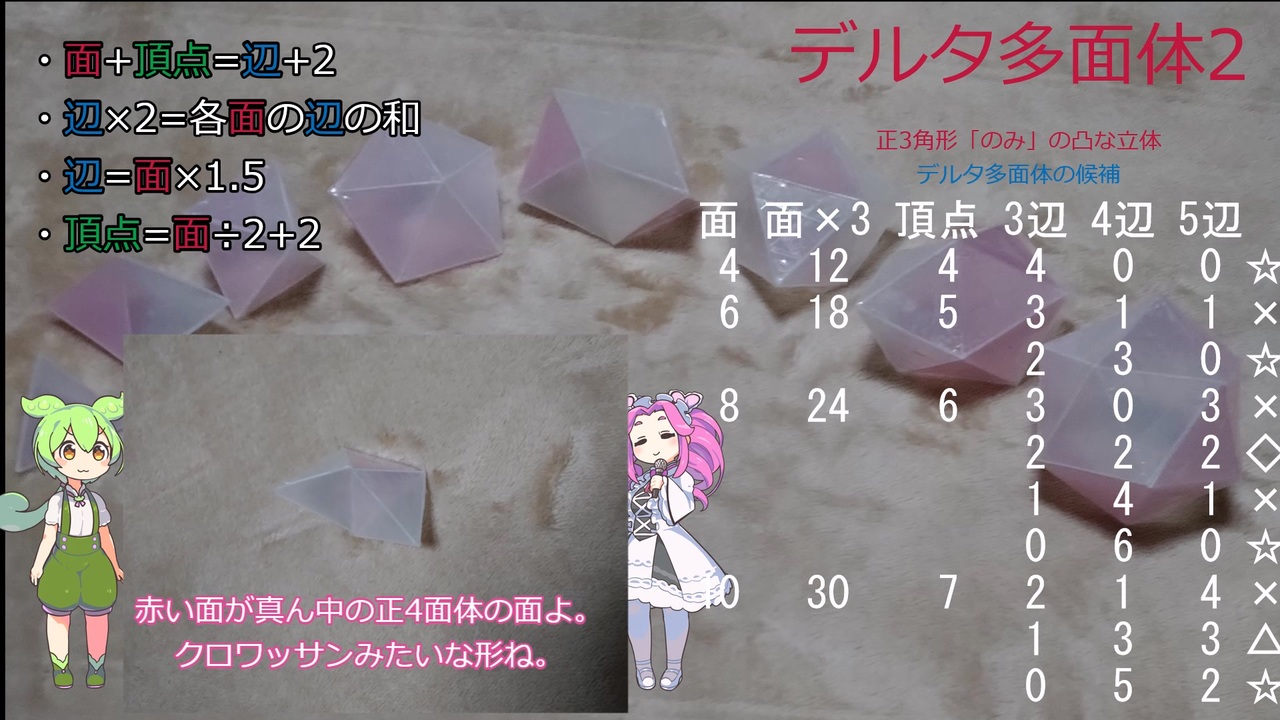
デルタ多面体について考えていきます。
デルタ多面体は8種類(4,6,8,10,12,14,16,20面体)あります。面の数は全て偶数で18面のはありません。
正多面体は4,8,20面体の3種類です。
4面体は正3角錐です。
n角錐は側面が正3角形n枚と底面の正n角形1枚なので、
正4角錐や正5角錐は正3角形以外の面を含んでしまいます。
6,8,10面体は双錐で、それぞれ双正3角錐、双正4角錐、双正5角錐です。
双n角錐は正n角錐2個を底面で接合した立体で、正3角形2n枚でできる立体です。
底面の正n角形は接合する時に消えるので、双正4角錐、双正5角錐もデルタ多面体になります。
また、正n角錐は頂点にn枚の正3角形が集まるのでnは3,4,5のみです。
正8面体は正多面体であり、双錐でもあり、反角柱でもあり、
正四面体の辺の中点を結んだ立体でもある特徴の多い立体です。
n角柱は天面・底面が正n角形で2枚と、側面の正方形がn枚です。
正方形を正4角錐で置き換えると、正方形1枚が正3角形4枚になります。
正方形は3枚あるので12枚と天面と底面の2枚を足して14枚です。
16,20面体は双錐反角柱で、それぞれ双錐正4反角柱、双錐正5反角柱となります。
また、20面体は正多面体です。
双錐正n反角柱は、正n反角柱の天面と底面に正n角錐を付けた立体です。
正n反角柱は、天面・底面が正n角形で互いに1/2n周ずれています。
側面は正三角形2n枚で、天面・底面の片方と辺を共有し、他方は頂点を共有します。
よって、双錐正n反角柱は天面・底面の正n角錐で正3角形2n枚と正n反角柱の側面の正3角形2n枚で正3角形4n枚です。
反角柱はnは3以上ですが、角錐の方がn=3,4,5なので、候補は3,4,5の3つです。
しかし、n=3の時は、正3角錐(正4面体)と正3反角柱(正8面体)の面のなす角が180°になるので、これからは除外されます。