
奇数 k を Sierpinski Number と定義するのであった。
そのような k は紛れもなく存在するのであるが、逆に n を固定して k を動かした場合、どんな n に
対しても常に合成数を与えるようには出来ない。即ち、どんな n に対しても必ず値が素数となるような
k が無限に存在する。(これは Dirichlet の算術級数の定理から明らか)
したがって n を与えれば、最小素数を与える k が必ず存在する。そのときの k は n に対してどんな
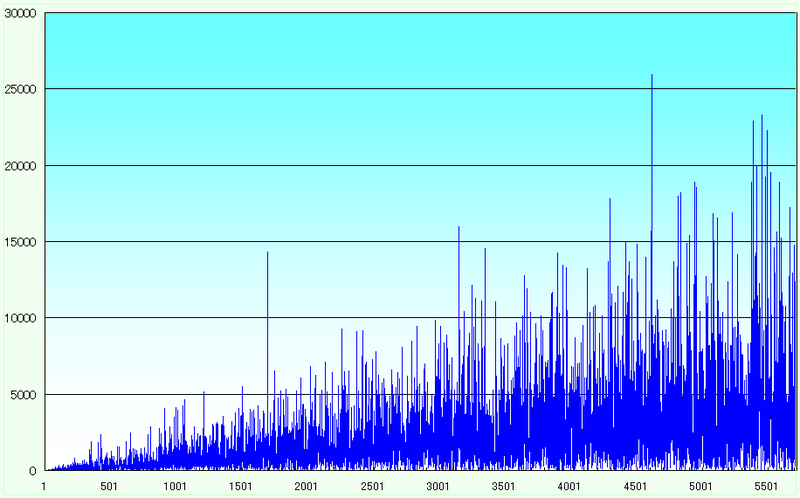
振る舞いをするだろうか図式化したのがこのグラフである。
絶対値が大きくなるにつれて素数の密度は希薄になっていくから、n が大きくなるにつれて最小素数は
次第に大きくなると考えられる。つまり k の値も上昇すると予測される。その予想を裏付けるのが
青色のグラフである。
グラフは非常にギザギザした形状を示している。n = 1,700 付近に突出した値が見られるが、これは
n = 1,695 のときの k = 14,319 に対応する。即ち k * 21695 + 1 が初めて素数となるのは
k = 14,319 であることを示している。
全体的にはグラフの帯となる中心部分は、上下動を反復しながら少しずつ上昇しているように思われる。
些か乱暴であるが k と最小値を与える n を一次近似することを考えた。最小値を与える n の平均値を
求めてそれを k で割った値を縦軸に取った推移が赤色のグラフである。
値 k が小さいうちは、変動が非常に激しい。荒い上下動を繰り返し、n が1,000 付近に達してもなお
落ち着く気配がない。指数としては 1,000 程度だが、実際の数値は 300 桁を軽く超える大きさである。
n が1,500 を超えたあたりからこの比は漸く変動が小さくなり、グラフを見る限り 2.8 付近のある値に
収束しそうな気配である。
この比率が 2.8 付近に収束するか否かはもちろん、特定の値に収束するかどうかすら不明である。まだ
調査範囲が広くはなく、もっと先に進んだところで 2.8 ラインから大きく外れるかも知れない。
この定数を仮定すれば、n が非常に大きい値を取る場合、k をどのあたりまで大きくすれば最小素数が
得られるかの目安をたてることができる。例えば n = 28,000 付近の値を取った場合、k は平均的には
10,000付近であるから、その値まで調べることによって素数を得るまでの平均時間が判明する。
しかし平均値が分かったところで、ある n に対して最小の素数を与える k がどう与えられるかには
全く貢献しないのは、素数定理を元にした素数分布と同じである。
n に2の大きなベキ乗を取った場合で k の最小値を考えてみよう。
n = 16384 (214) , n = 32768 (215) , n = 65536 (216) の場合では、それぞれこの順で k の最小値も
大きくなると考えられる。しかし実際には最小素数は
6223 * 216384 + 1
3493 * 232768 + 1
1063 * 265536 + 1
が条件を満たす最小だから、全く予想に反する結果となっている。n = 65536 の場合、先の収束比を
仮定すれば 65536 ÷ 2.8 ≒ 23400 だから k が2万項を超えて走査しなければ最小素数が見つからない
可能性があると言える。実際は小さなところに最小素数が見つかったのは、全く幸運だったのだろう。
実際、この次のケースである n = 131072 では、k は20000 を超えて調査しているにも関わらず、なお
最小素数が出力されて来ないのだった。
(後日の調査で、50655 * 2131072 + 1 が最小素数であることが判った)