2020/09/16
z軸周りの断面2次モーメントは
こうなります。2項目は定義です。
先程のIzの式を
となり、縦長に使った方が応力が1/2になることがわかります。
図心を通るz軸に関する断面二次モーメントをIz、上図のようにy=eの位置にあるz軸に平行な任意のz'軸に関する断面2次モーメントをIz'として、Aを断面積とするお、以下の式が成り立ちます。
2.加算定理
さて、3つのエリアに分割して考えます。
A3エリアのI3はI1と同じです。
もし、断面積がH型ではなく、長方形だったとすると
また解説を書くのは面倒なので、流れだけ書いてから解説を貼ります…
最後の結果を見ると面白いことがわかります。
おはようございます！
だいぶあいてしまいました💦
前回、曲げモーメントに対して発生する曲げ応力を導出しました。その際はモーメントの釣り合いを使いましたが、断面2次モーメントが含まれていたかと思います。
今回は簡単な形状の断面2次モーメントを計算します。
こうなります。2項目は定義です。
つまりIzは、高さhの3乗、幅の1乗に比例することがわかります。
では問題。
先程のIzの式を
h→2a, b→a
h→a , b→2a
としましょう。
するとIzが左から2a^4/3, a^4/6 とわかります。
最大応力は
σ = M/Iz ×y
ですから、最大応力は左から
感覚的にわかりますよね…
ここからは、断面二次モーメントを求めるための有用な公式の紹介です。
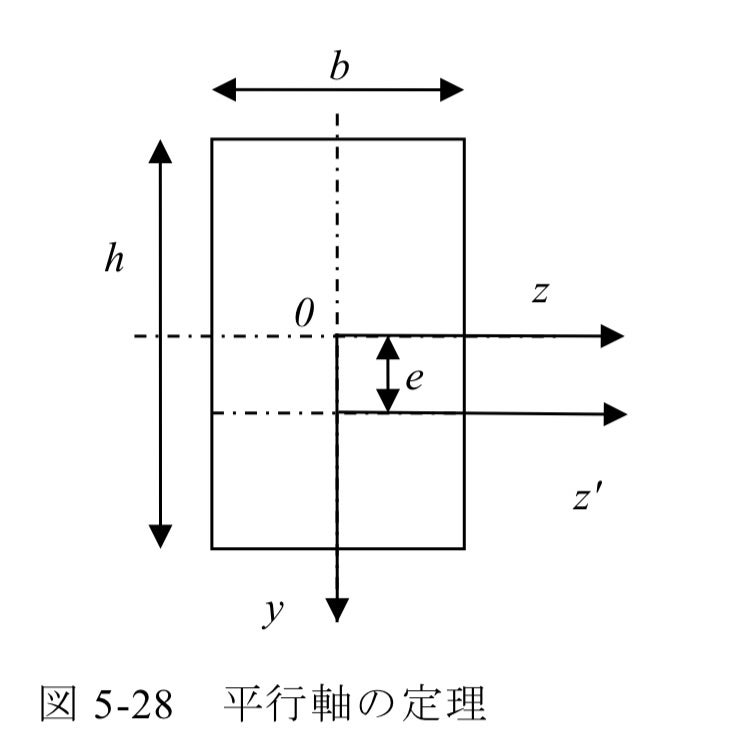
1.平行軸定理
断面積Aの図形を分割して断面全体を和または差で表すと、全断面積は
A= A1±A2....±An
となり、分割した断面のz軸に関する断面2次モーメントをそれぞれI1, I2,...Inとすると
全断面2次モーメントは
I = I1 ± I2 ±...± In
これらを使って問題を解きましょう。
さて、3つのエリアに分割して考えます。
まずは上のA1について。
まずこのエリアの断面2次モーメントは(あくまでのこのエリアでの話)
高さa/2なので、
a^4/96
です。実際の図心はO点なので、平行軸の定理を使って移動します。
A2エリアについてです。これは簡単。
I2 = a^4/24
よって
もし、断面積がH型ではなく、長方形だったとすると
I = 2a^3/3となります。
長方形→H型で…
断面積は2a^2→1.5a^2と25%減少
断面2次モーメントは6.25%しか減少していない
ことがわかります。
つまりコストを抑えながら強度は保証できるということですね。
さて最後。
また解説を書くのは面倒なので、流れだけ書いてから解説を貼ります…
まずはねじれの剛性に関わる断面2次極モーメントIρを求めます。
Iρ = Iy + Iz
が成り立ち、円形なのでIy=Izとなります。
これで半径rの時のIzやZが求まります。
ほぼ中実断面は求まったので、あとは加算定理を使って中空形状を求めるのみです。
最後の結果を見ると面白いことがわかります。
それは中空にすることで、質量は3/4倍になるが、断面2次モーメントと断面係数は15/16倍にしかなっていないということです。
15/16って1.067ですから、曲げ応力はそんなに大きくならないですよね。
つまり軽量化できているということです。
しかし中空断面の肉厚を薄くしすぎると、座屈が起こったりと破壊モードを考慮する必要があります。
長かったですが、今回はここまで！
次回は梁のたわみの話です！
では！
