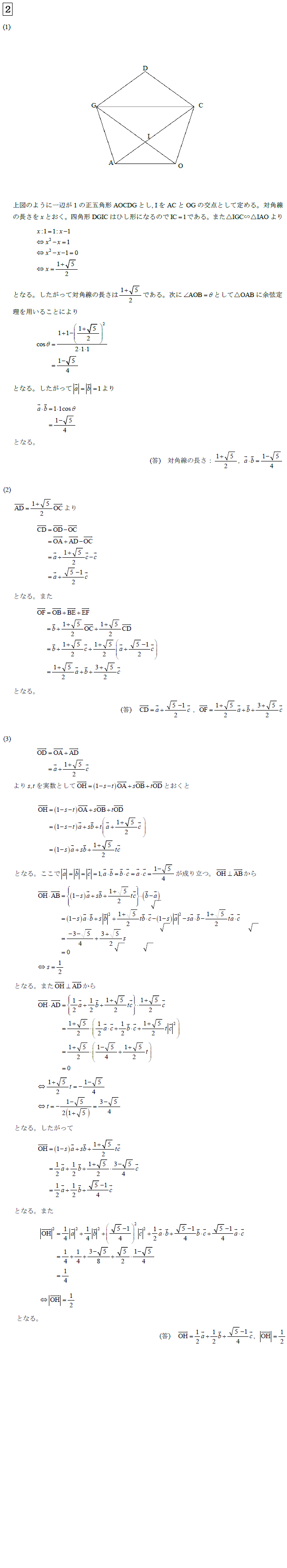2016年
東北大学・経済(後期)
数学 第4問
おはようございます,ますいしいです![]()
受験生の皆さんを心より応援しております![]()
それでは,まずは偉人の言葉からです![]()
![]()
『……今日,数学は
社会の生産力へと
変わった.』
(B・グネジェンコ,ロシアの数学者)
それでは,最初は解答を見ずにチャレンジしてみてください![]()
![]()
(問題)
(※ 時間の目安) (1)10分 (2)8分 ![]()
An equiateral triangle
(ますいしいの解答)
コメント;いかがでしたでしょうか?楽しんで頂けましたでしょうか?
(1) やはり,ここは“ベクトルの内積”に持ち込むのがよい
でしょう![]() “余弦定理”でもいけそうですが計算量が
“余弦定理”でもいけそうですが計算量が
内積よりかさむ感じですね![]()
(2) 理系であれば,“商の微分法”に持ち込んでもよいの
でしょうが,これも計算量がかさみそうです![]()
ということで上のような式変形を施せば最終的には
“平方完成”に持ち込めます![]()
頑張れ,受験生![]()
頑張れ,大谷選手![]()
それでは、次回をお楽しみに![]()
by ますいしい
下の書籍は、“計算力”を
身につけるのに、お勧めです![]()