2001年
東京工業大学・理類(前期)
数学[４]
おはようございます，ますいしいです
受験生の皆さんを心より応援しております
それでは，本日もまずは偉人の言葉からです
『幾何学的な方法は何に
でも適用できるわけで
はないと主張するのは
誤りであるが,しかしそ
れを何にでも適用する
のはよくないというの
は正しい.何事もそれぞ
れ独自に扱われなけれ
ばならない.たとえば幾
何学的方法は,行儀作法
の躾に用いるには愛想
がなさすぎるし,われわ
れの言葉はそっくり頼
りにするには不完全す
ぎよう…….
しかし,これはたまたま
用いるのを諦めざるを
得ないようなことにな
ると,必ず思い出すもの
で,つまり知性のための
一種独特な指針であり,
想像力に対する歯止め
である．』
(Ｄ・ディドロ,フランスの哲学者で文学者,1731-1784)
今回の下の問題はこの年
一番の『難問』だと思い
ます
とても時間内に解き
切るというのは厳しいと
思います
私も何時間もかかりま
したみなさんは,この問題
にどのように取り組まれ
ますでしょうか
何かよい
解法がありましたらコメ
ントを頂けたら嬉しいか
ぎりです
それでは，最初は解答を見ずにチャレンジしてみてください
（問題）
（※ 時間の目安） 
Elementary
geometry
（ますいしいの解答）
コメント；いかがでしたでしょうか？楽しんで頂けましたでしょうか？
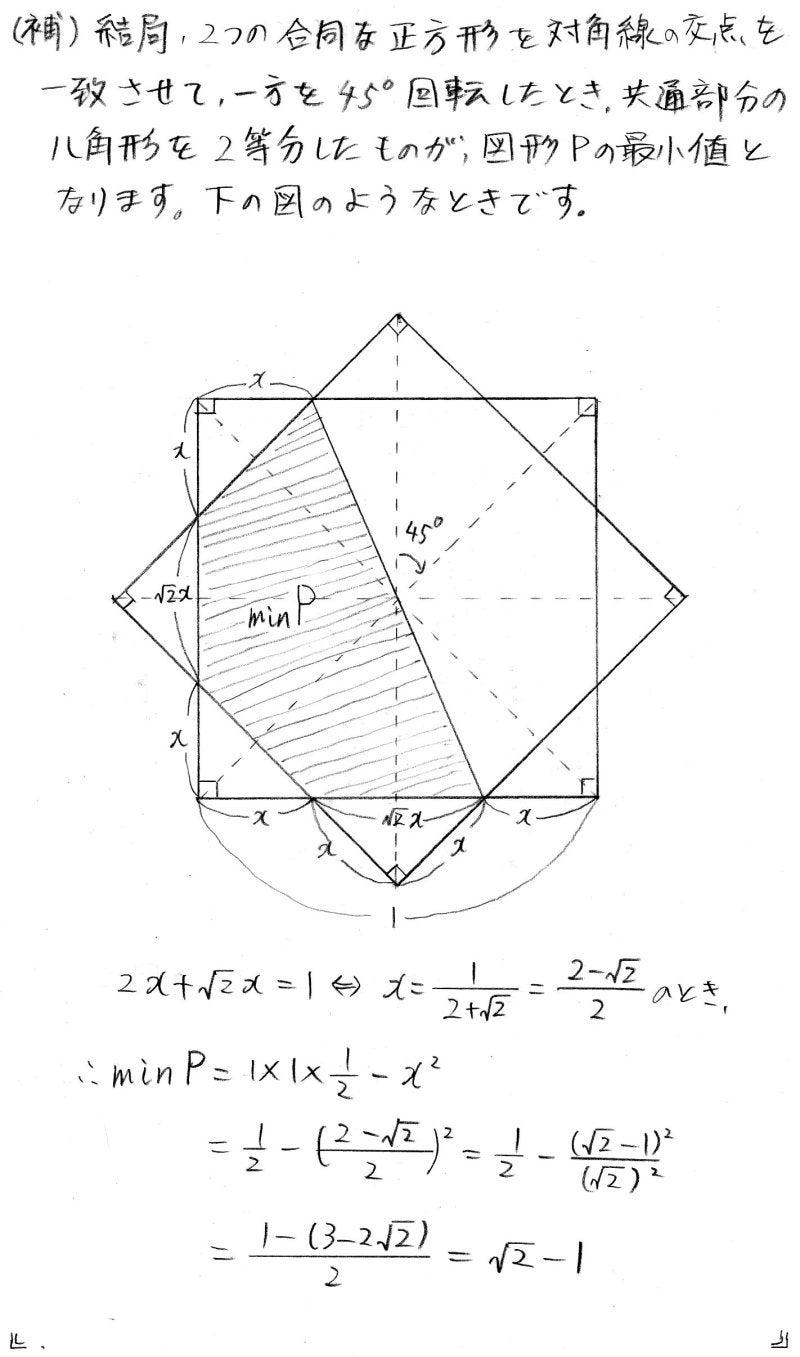
直観的には，（補）で示したような場合であることはわかる
のですが，これをどのように答案として組み立てて行くの
かが問題です “ますいしい”は，上のようにやってみま
したが，議論の粗いところもあります こうした方がよい
というのがありましたらコメントを頂ければと思います<(_ _)>
それでは、次回をお楽しみに
ｂｙ ますいしい
