２００８年 早稲田大学・理工学部 数学 第１問
こんにちは，ますいしいです
本日第２弾目のアップです
本当に入試が近づいてきています
少しでもお役に立てるようがんばります
今回の問題で（２）の求積は，かつてＡ・Ｊ氏が，“松かさ方式”などとと呼んでいましたね
ここでは，さらに“別解”をつけ加えました どうぞ，二通りの解法をお楽しみください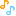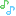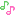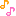
それでは，まずは本日第２回目の偉人の言葉からです
『 幾何学的真理は，ある意味で物理的真理に対する漸近線のよう
なものである．すなわち，前者は後者にかぎりなく近づくが，完全に
合致することは決してないのである．』
（Ｊ・ダランベール，フランスの数学者・物理学者で哲学者，
1717 - 1783）
それでは，最初は解答を見ずにチャレンジしてみてください
（※ 時間の目安） （１）１２分 （２）１３分 
（ますいしいの解答）
コメント；いかがでしたでしょうか？楽しんで頂けましたでしょうか？
（１） 実は， √ｘ ＋ √ｙ ＝ √ａ は，放物線です
“別解”として，放物線であることを，“回転の一次変換”を使って，
示してみました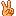
そうすると，いとも簡単に“面積”，“体積”は，
求まってしまいます
（２） “円錐の側面積” ＝ “（母線）×（底面の半径）×π”，です
それでは，次回をお楽しみに
ｂｙ ますいしい
大学受験 ブログランキングへ
