ドールハウスを作っていると、フリーハンドで作れる物もあれば
逆に図面作って組み立てた方が楽な物も出てきます。
特に珈琲ポットとか、バケツとか・・円錐台形の物って結構ありますよね^^
バルサ等の木材を削ってアバウトに形を作り上げても良いのですが・・
どーせだったらきちんと作りたい!!そんなこと思いませんか^^?
図形って大概の物は計算で割り出せます。
それこそ中学とか高校で習ったはず・・w
でも、実生活の中で計算することってあまり無いもんね~。
・・と言い訳ですけど、すっかり計算忘れてましたw
てなことで、少し説明しますね^^
例題として、上面の直径40㎝、下面の直径60㎝、高さ40㎝の円錐台を
割り出してみましょう♪
円錐台の考え方は、円錐の一部分が切り取られた形であるという事を基に進めます。
円錐台を基の円錐にして、それを横から見た三角形からその斜辺を割り出していきます。
まず
切り取られた部分の斜辺をC2、
円錐台部分の斜辺をC1、
オレンジの直角三角形の底辺をA
その垂直辺をB
円錐台(台形)の上面半径をr1
円錐台(台形)の下面半径をr2とします。
Aは円錐台の上面と下面の差、Bは円錐台の高さですから、三平方の定理からC1が割り出せます。
この例の場合、41.2310になります。
オレンジの三角形と青い三角形の部分は縮尺が異なる同じ形なのですね^^
その大きさの比率からC2斜辺の長さが割り出せます。
この例の場合、それぞれの三角形の底面にあたる部分r1とAの比率が2:1。
・・ということは、C2:C1も2:1なので
C2は82.462となります。
円錐台は切り開くと扇形になりますから、
この場合、C2+C1が半径の円の一部分。
扇形の角度θは扇形の弧の長さと
円周の長さの比で求められますね^^
扇形の内側の弧の長さとr1は同一なので
そこからC2を半径とする円とr1の比率を求めれば、角度が求められます。
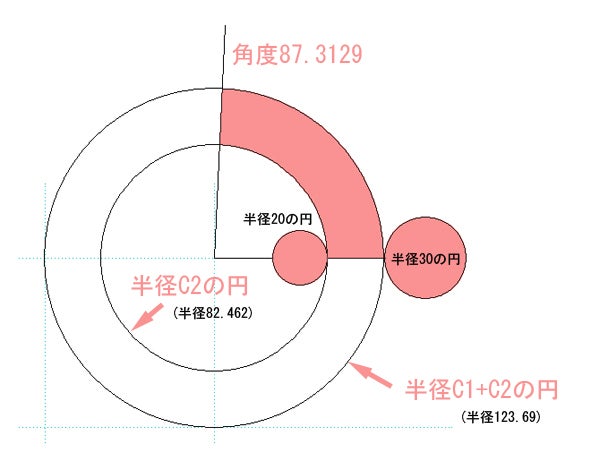
この場合、87.3129となります^^
これらを基に図形を書くと、
①C1+C2を半径とする円を書く
②その内側にC2を半径とする円を書く
③そのうち角度θで線を引く
④半径r1の円を内側に書く
⑤半径r2の円を外側に書く
はいこれで出来上がり~♪
上の図のピンクの部分が円錐台の展開図になります^^
アイスクリームのカップなんかを作っても面白いですよね~^^
因みに・・図形を作るまでは簡単ですが、これを紙に印刷して切り張りして組み立てると
意外に丸く作れないです^^;
結果的には木材でアバウトな型作って、その形を利用して円錐台に仕上げていくのが
良いのかもしれませんね^^

にほんブログ村

逆に図面作って組み立てた方が楽な物も出てきます。
特に珈琲ポットとか、バケツとか・・円錐台形の物って結構ありますよね^^
バルサ等の木材を削ってアバウトに形を作り上げても良いのですが・・
どーせだったらきちんと作りたい!!そんなこと思いませんか^^?
図形って大概の物は計算で割り出せます。
それこそ中学とか高校で習ったはず・・w
でも、実生活の中で計算することってあまり無いもんね~。
・・と言い訳ですけど、すっかり計算忘れてましたw
てなことで、少し説明しますね^^
例題として、上面の直径40㎝、下面の直径60㎝、高さ40㎝の円錐台を
割り出してみましょう♪
円錐台の考え方は、円錐の一部分が切り取られた形であるという事を基に進めます。
円錐台を基の円錐にして、それを横から見た三角形からその斜辺を割り出していきます。
まず
切り取られた部分の斜辺をC2、
円錐台部分の斜辺をC1、
オレンジの直角三角形の底辺をA
その垂直辺をB
円錐台(台形)の上面半径をr1
円錐台(台形)の下面半径をr2とします。
Aは円錐台の上面と下面の差、Bは円錐台の高さですから、三平方の定理からC1が割り出せます。
この例の場合、41.2310になります。
オレンジの三角形と青い三角形の部分は縮尺が異なる同じ形なのですね^^
その大きさの比率からC2斜辺の長さが割り出せます。
この例の場合、それぞれの三角形の底面にあたる部分r1とAの比率が2:1。
・・ということは、C2:C1も2:1なので
C2は82.462となります。
円錐台は切り開くと扇形になりますから、
この場合、C2+C1が半径の円の一部分。
扇形の角度θは扇形の弧の長さと
円周の長さの比で求められますね^^
扇形の内側の弧の長さとr1は同一なので
そこからC2を半径とする円とr1の比率を求めれば、角度が求められます。
この場合、87.3129となります^^
これらを基に図形を書くと、
①C1+C2を半径とする円を書く
②その内側にC2を半径とする円を書く
③そのうち角度θで線を引く
④半径r1の円を内側に書く
⑤半径r2の円を外側に書く
はいこれで出来上がり~♪
上の図のピンクの部分が円錐台の展開図になります^^
アイスクリームのカップなんかを作っても面白いですよね~^^
因みに・・図形を作るまでは簡単ですが、これを紙に印刷して切り張りして組み立てると
意外に丸く作れないです^^;
結果的には木材でアバウトな型作って、その形を利用して円錐台に仕上げていくのが
良いのかもしれませんね^^
にほんブログ村