以前の記事に関連するテーマです。
最近は平面図形の移動だけでなく、立体図形の移動について考えさせる問題も少しずつ出題されるようになってきています。
たとえば今年の出題例として次の問題があります。
下の図のような直方体の箱と円柱と円すいがあります。円周率は²²⁄₇として計算しなさい。（清風南海2024）
①［図1］のように、直方体の箱の中で円柱を立てた状態で動かします。円柱が通過できる部分の体積を求めなさい。
上から見ると、円柱は下図左のグレーで示した部分を通過できる。これは①正方形全体から②4つの角の白い部分を取りのぞいた形
- ここで②4つの角の白い部分の面積の和は上図右の赤い部分（正方形から円を引いた形）の面積としてまとめて計算できる。これを計算すると 2×2－1×1ײ²⁄₇＝4－²²⁄₇＝⁶⁄₇㎠
- したがって左のグレー部分の面積は 6×6－⁶⁄₇＝35⅐㎠
よってこれを底面積とする高さ7㎝の立体の体積が円柱が通過できる部分の体積だから 35⅐×7＝246㎠
②［図2］のように、直方体の箱の中で円すいを立てた状態で動かします。円すいが通過できる部分の体積を求めなさい。
まず求める立体のイメージ図を考えると次のような感じになる。
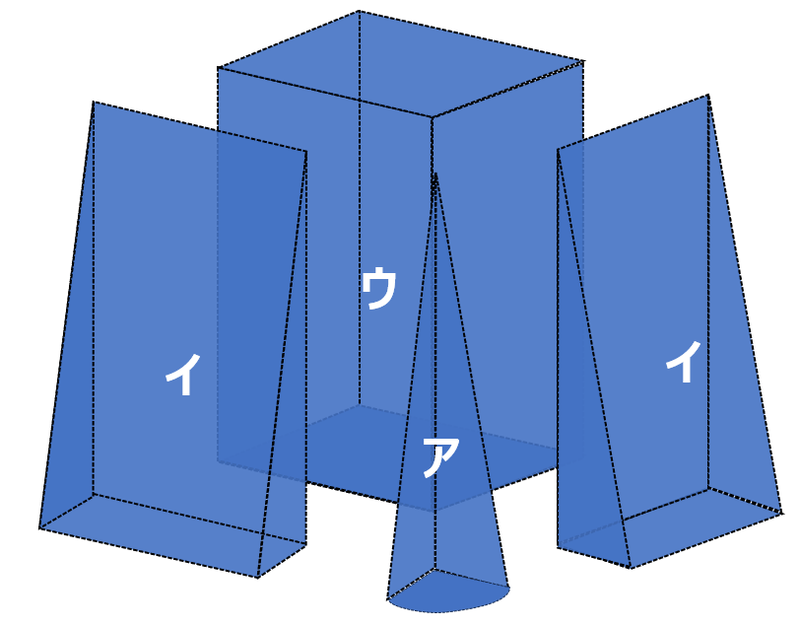
この立体の手前の部分を取り出すと次の3つの立体に分解できる。
- ア…これを4つ合わせるともとの円すいになるという立体
- イ…三角柱（たて1㎝、横7㎝の直角三角形を底面とみて高さ4㎝）
- ウ…四角柱（底面は1辺4㎝の正方形、高さ7㎝）
それぞれ体積を計算すると
- ア…4個分で 1×1ײ²⁄₇×7÷3＝7⅓㎤
- イ…4個分で 1×7÷2×4×4＝56㎤
- ウ…4×4×7＝112㎤
よって円すいが通過できる部分の体積は 7⅓+56+112＝175⅓㎤ 
