今から紹介するものは『ロシア農民式かけ算』であります。その昔、ロシアの農民たちの間で伝統的に採用されていた計算方法のようです。なかなか面白い原理なので、塾の授業で小学生に紹介しようと思っています。
ネタとしては有名なので、もし知っている方がいらしたら、改めて原理を考えていただきたいと思います。
ちなみに、これについて私は十年以上前に本で紹介されていて知ったのですが、ロシアのいつの時代のことか失念してしまいました。インターネットで調べてみたものの、なかなか探せなかったので、ご存じの方がいましたら教えていただければ幸いです。
で、さっそくそのやり方ですが、例えば「10×38」というかけ算をするとき、次のようにします。
①まず、右側の数は半分にしていきます。ただし、当時のロシア農民の人たちに小数の概念がなかったため、割り切れない場合は切り捨てた値にします。例えば19の半分は９とするわけです。右側の数が１になるまでこれを繰り返します。左側の数は２倍にしていきます。
②次に、右側の数が偶数になっている行を、左の数もろとも線で消します。
③最後に、右側の数で残っているものを全て足し算すると答えが出ます。
さて、どうですか？
「お！？ すごい、どうして？
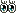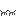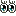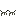
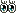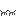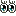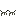」と思ってくれたらよいのですが。これに関して、いろいろ調べてみると「２進法」、つまり電卓の中で実際にされている処理方法と同じだということで、解説が書かれているものを多く見ます。
ただし、それだとまず２進法を理解してからでないと厳しいですよね。
そこで今回は、そうでない解釈でこのかけ算の原理を見ていきます。
これからヒントとなる別の問題を出しますので、このロシア式かけ算でその問題を解いてみて下さい。
５×32
はい、出来ましたか？
実際にやってみると図のようになりますね。
これを見て何かピンとくるものがあるでしょうか。
え、なになに？
「片方を２倍してもう片方を２で割ってるんだから、答えが変わらないのは当たり前じゃん！」ですって？
はい、その通り
です。根本の原理は「問題の書き換え」なんです。それがよくわかる例がこの「5×32」の例。右側が全て２で割り切れるため、単に１行ごとに問題を書き換えているだけということになるんですね。で、必要のなくなった行は消すということ。
残る問題は、右の数が２で割り切れなかったときですね。切り捨てた値にし、その行は消さずに残しておくと…。なぜでしょうか？
（※ここから完全に解説してしまうので、自力で解決したい人は以降を見ずにガマン！）
では、最初の問題に戻って解説しましょう。
２行目の「20×19」を３行目で「40×9」に書き換えた場合、本来は40×9.5でなければならないはず。でも切り捨てて40×9にしてしまったので、「40×0.5＝20」だけ少なくなる式に書き換えていることになるのです。
以降は、同じようにまた書き換えていく。もし後で足さなければならないものが出てきたらそのつどチェックしていき、最後に合計するという具合です。
どうですか？ なかなか面白い仕組みですよね。
ちなみに、現在のロシアの小学校では階段がこんな風になっているとか（※写真は秒刊SUNDAYより）。
計算一つとっても、原理とか仕組みというものはしっかり考える習慣をつけたいですよね。身近なところで言えば、「分数で割り算するときに、分母と分子をひっくり返してかけ算にするのはなぜだろう？」とか。
当たり前だと思っていることにこそ、今一度スポットを当ててみてはいかがでしょうか。
人気ブログランキングへ