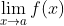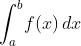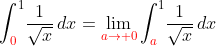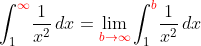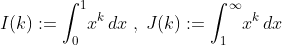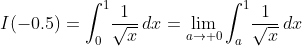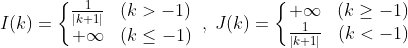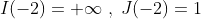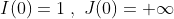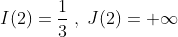※極限の表記
ここでは
f(x)のx→αのときの極限を
lim[x→α]f(x)
と表記することにする。
※定積分の表記
f(x)のaからbまでの定積分を
∫[a〜b]f(x)dx
と表記することにする。
○広義積分
積分区間内のいくつかの点で発散したり、積分区間の長さが発散したりするような定積分を広義積分という。
広義積分は定積分の極限として定義されて、ある値に収束することもあれば発散することもある。
例1)
∫[0〜1](1/√x)dx
=lim[a→+0]∫[a〜1](1/√x)dx
例2)
∫[1〜∞](1/x²)dx
=lim[b→∞]∫[1〜b](1/x²)dx
○記号の定義
簡単のため、
I(k)=∫[0〜1]xᵏdx
J(k)=∫[1〜∞]xᵏdx
とする。
これらは場合に応じて適切に広義積分で定められることとする。
例えば、
I(-0.5)=∫[0〜1](1/√x)dx
は、1/√xがx=0で定義されないが
I(-0.5)
=lim[a→+0]∫[a〜1](1/√x)dx
とすればよい。
○I(k)とJ(k)の収束・発散
便宜上、広義積分でない通常の定積分に対しても「収束する」「極限値」という言葉を用いる。
結論だけいえば、
I(k)はk>-1のときに、J(k)はk<-1のときに収束し、その極限値は1/|k+1|である。
それ以外のときは、どちらも+∞に発散する。
例えば、
I(-2)=+∞,J(-2)=1
I(0)=1,J(0)=+∞
I(2)=1/3,J(2)=+∞
である。
※証明の概要
ただの計算で煩雑になるためここでは証明しない。(高校数学までの知識ですぐにできる。)
I(k)は、k>0のとき通常の定積分として計算できる。その他の場合は
①k<-1,②k=-1,③-1<k<0,④k=0
の4つに場合分けして、x=0で被積分関数が発散する広義積分として計算すればよい。
J(k)は、積分区間が+∞までの広義積分として計算する。そのとき、
①k<-1,②k=-1,③-1<k<0,④0≦k
の4つに場合分けして計算すればよい。
(I(k)でt=1/xとした置換積分を考えてもいいかもしれない。)
(2018/04/22:数式を追加)