図1.イジングモデル
図1のように、N個の粒子が持つスピンSi=±1を、それぞれ↑=+1、↓=-1として格子状に配列して、スピン間の最近接相互作用が働くとしたものをイジングモデルと呼ぶ。この系のエネルギーは
で与えられる。ここで、Jはスピン間相互作用であり、hは磁場の強さh=μBを示す。μは磁気モーメントであり、Bは磁束密度である。このエネルギーの第一項は系内部のスピンの寄与であり、第二項は外部磁場の影響である。この系について解くために、スピンを平均値mと平均からのずれδSiとして
と置き換える。これより、式(1-1)は
となる。ここでzは、iに隣接する結合の数であるため、図1のように2次元の場合はz=4となる。このzを用いると、第二項の和は結合の度に1つずつ現れるため
と書き直せる。これに、再び式(1-2)を用いると
となる。ここまでの処理は、解となるはずの平均値を先に仮定し、一体問題に帰着させることで、式(1-5)を自己無撞着な式に書き直した。このような手法は平均場近似と呼ばれる。
統計力学の関係式から分配関数
について、平均場近似によって得られたエネルギー(1-5)を用いて求める。ここで、βはボルツマン定数と温度の積の逆数1/kBTである。これより、式(1-6)は
となる。さらにこれを用いて、自由エネルギー
について求めると
となる。この自由エネルギーはエネルギーの原理から、最小状態に落ち着くため、パラメータmについて微分して0になる最小値を求める。よって、式(1-9)から
となり、mについて整理すると状態方程式
を得る。□
出典:HIDETOSHI NISHIMORI. Statistical Physics of Spin Glasses and Information Processing An Introduction
P1 1.MEAN-FIELD THEORY OF PHASE TRANSITION
HHidetoshi Nishimori. Gerardo Ortiz. Elements of Phase Transitions and Critical Phenomena
P16. 2 Mean-field theories 2.1 Mean-fiels approximation
―――――――――――――――――――――――――――――――――――――――――――
昨今、注目を集める人工知能のモデルである、ニューラルネットワークについて議論していく。その基礎であるイジングモデルについての理解を深めるため、今回は解析的に解ける形に置き換えた平均場近似について求めた。
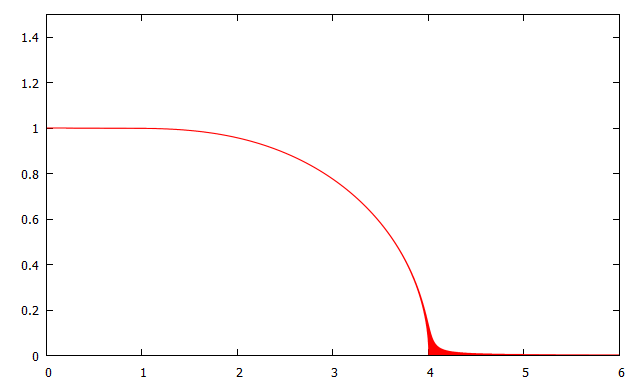
今回得た式(1-11)はパラメータmについての状態方程式であるが、mの本来の意味を考えると、スピンの平均値であることから系の磁化を示すことがわかる。このことを踏まえた上で、2次元の場合で式(1-11)の概形を数値的に示すと図2のようになる。図を見れば明らかにように、kBT<4のときm>0となり、kBT>4のときm=0となる。これは、温度が低い領域では自発磁化を持ち、温度が高い領域では磁化が失われることを示し、この系が強磁性相と常磁性相で相転移を起こすことを意味する。温度が高い状態、すなわち外場からエネルギーを受け取り乱雑さが増すことで、常にスピンの向きが入り乱れている状態と、温度が低く、内部磁場にスピンが引っ張られて、同じ方向に向いてる状態と理解できるだろう。このように、イジングモデルは非常にシンプルな要素で物質の相転移を示すことに成功したモデルである。
ニューラルネットワークの想起のメカニズムは、この相転移の制御によって、系に記録した状態に到達させることである。今回の議論を前提として、以後の議論を進めていく。
図2.縦軸m、横軸kBT、z=4のmについての状態方程式
 |
Statistical Physics of Spin Glasses and Informa...
12,125円
Amazon |