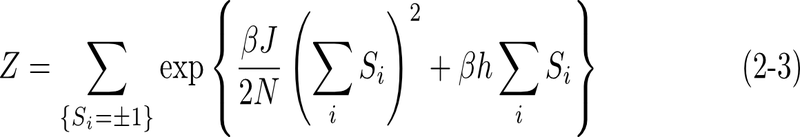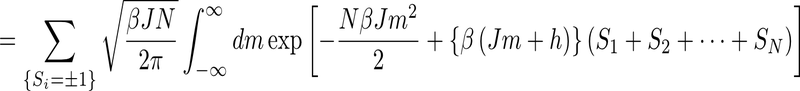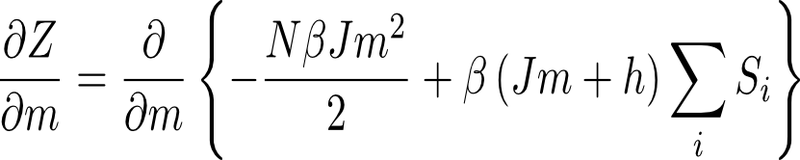ニューラルネットワークの理論2:無限レンジモデルの厳密解 | NOTE
AmebaAmeba 20th Anniv.ホームピグアメブロ
芸能人ブログ人気ブログ
新規登録
ログイン

NOTE

備忘録

ニューラルネットワークの理論2:無限レンジモデルの厳密解

図1.イジングモデル

 

　今回の無限レンジモデルは、図1のイジングモデルとは異なり、最近接相互作用ではなく、iとjの全ての組み合わせについて数え上げるとして、エネルギーを

と定義する。ここで、第一項の1/2は数え上げの重複を取り除くためであり、1/Nは示量変数であるエネルギーの次元をO(N)に揃えるためである。前回と同様に、分配関数について求めたいので式(2-1)の第一項の総和を書き直して

　　

とする。ここでβJ/2は定数であり、系の大きさであるNに対して十分小さいため、これ以降無視する。この式(2-2)を前回の式(1-6)

に代入すると

となる。ここで、ガウス積分から得られる公式

に

として代入すると、式(2-3)の指数関数中の第一項は

となり、これを式(2-4)に代入すると

　　

　　

　　

となる。さらに、鞍点法により近似的に積分を除くと、最終的に分配関数は

と求められた。この式(2-6)から、指数関数の係数を無視して、前回の式(1-8)

を用いて、自由エネルギーを求めると

となる。式(2-7)から、パラメータmについての最大値を求めると

　　　

となり、mについて整理すると状態方程式

を得る。このmの意味について考えると、式(2-5)の最初の式に鞍点法を適用して、mについての最大値を求めることで

　　　

となり、mについて整理すると

を得る。これは、系のスピンの平均であり、すなわちパラメータmは磁化を意味することがわかる。□

出典:HIDETOSHI NISHIMORI. Statistical Physics of Spin Glasses and Information Processing An Introduction

P1 1.MEAN-FIELD THEORY OF PHASE TRANSITION

 

HHidetoshi Nishimori. Gerardo Ortiz. Elements of Phase Transitions and Critical Phenomena

P30 2 Mean-field theories 2.5 Infinite-range model

―――――――――――――――――――――――――――――――――――――――――――

　各スピンが他の全てと相互作用するとしたため、イジングモデルの次元を無限にしたと言える。また、相互作用間の距離を問わず、全てのスピンが相互作用する。このことから無限レンジモデルと呼ばれる。このモデルから得られた状態方程式は、前回のイジングモデルの平均場近似解で得られた結果と関数の形が同じである。若干の差異はあるが、前回の式(1-11)

から、隣接する結合の数をz→Nとして、次元を揃えるためにJ→J/Nと変数変換を行えば式(2-9)となる。同様の結果が得られるのであれば、無限レンジモデルを解くということは、イジングモデルの平均場近似を解くことに等しいと言える。

　前回得た近似解とは違い、今回得た結果は厳密解であるということが非常に重要である。今後はより系を複雑に拡張して取り扱うため、このようにモデルを書き換えて解きやすい手法を取ることになる。