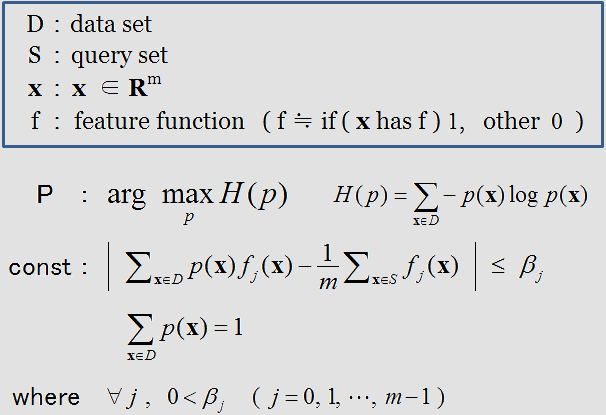ボスからのお達しで2回目のネタを書くことになりました。( 前回のネタはこちら )
聞く所によると3ヶ月に一回くらいのペースで本シリーズ?を書かねばならないのですが、1年後に果たして書くネタが残っているか、、、若干微妙な感じです。汗。
さて本日のテーマですが、" Set Expansionを利用した芸能人推薦の方法 " を紹介しようと思います。これは以前、株式会社 mixi 様との合同勉強会で発表した内容の補足的な話になっていまして、以下の発表スライドを先に斜め読みして頂けますと以降の話が分かり易いかと思います。
■ Set Expansion とは何ぞや?
Set Expansion とは 『 SEEDとなる部分セットを拡張・補完して、より完全なセット集合を作る 』 というタスクの事です。若干分かりに難いのですが、より平易に言うと 『 コーパスデータセットからクエリセットに関連する候補データを取得してくる 』 というタスクと言い換えても良いかもしれません。例えばクエリセットとして "塩ラーメン、豚骨ラーメン、味噌ラーメン" が存在する場合に、Set Expansion を行うと "醤油ラーメン" が補完されるというような感じです。
このようなタスクを行ってくれるシステムとして有名なものに、Google Sets [1] や SEAL [2][3] などが存在します。実際これらのシステムに、クエリとして先の例に挙げた3つのラーメンを入力すると、ちゃんと醤油ラーメンが返ってきます。( Google Sets の場合は miso, tonkotsu, solt を入力 )
遊んでいると中々面白いのですが、実世界においてもこのような機能は、例えば情報推薦や構造化文書の検索、農作物の栽培適地箇所の探索などといったケースで利用されています。今回は推薦という用途で、この Set Expansion を利用します。
■ Set Expansion のアルゴリズム
Set Expansion を実現するアルゴリズムは非常に多岐に渡るので、網羅的に述べる事は難しいのですが、例えば、コーパスベースによる手法 [4]、bootstrap的な手法 [5]、そして中でも BayesianSets [6] は近年非常に有名です。BayesianSets の利点は従来手法がややヒューリスティックであったのに比べ、背景理論が綺麗でしっかりしている事、そして何よりオンデマンドに計算結果を取得できる程に結果の作成が高速という点が優れています。
今回紹介するのは、BayesiabSets に似たような手法で MaxentSets [7] というアルゴリズムを紹介します。BayesianSets 程ではないのですが、割と高速で BayesianSets とはやや異なる推薦候補を得られる手法です。
■ MaxentSets
MaxentSets は最大エントロピー原理を使用した手法で、元々は動植物保全のための環境適合地を探す問題などでに使われていたそうです [8]。…と言ってもマニアック過ぎてイメージがあまり湧かないと思うので、ここで簡単な説明をしてみます。
学習データセットとして土地の集合を考えます。各データの素性には、その土地の年間降水量や平均気温、標高や傾斜方向、植生・土壌の性質などを使います。そこでクエリセットとして例えば、トウモロコシの栽培されている地域を複数選んで MaxentSet を実行すると、クエリセットの土地以外でトウモロコシが栽培できそうな土地が列挙される…という具合に利用できるのだそうです。他にも例えば、おいしいメロンを作るために良さげな場所とか、マグロの養殖に適した場所などといった事も分かるのかもしれません。
今回はデータセットとして芸能人を考えます。各データの素性としては土地に関する属性データではなく、他の芸能人との共起アクセスの頻度を使います。データ素性の具体的なつくり方は、既出のスライドにざっくり書いてあるので、そちらを参照して頂ければと思います。
さて、肝心の MaxentSets の中身の部分についてですが、背景知識のあるなしで随分説明の仕方が変わるので、最初に教科書的な説明を述べた後に、もう少し砕けた内容を述べるという順番で説明していきたいと思います。
◆ < 教科書的な説明 >
MaxentSets は下記のような条件を満たす確率分布 p の推定を行っています。
求める分布 p は目的関数の H 、すなわちエントロピーを最大にするような分布として決定されます。エントロピーの最大化とは事前分布を一様分布と仮定した場合にKLダイバージェンスを最少にすることと同値であり、要するに拘束条件を満たす以外はできるだけ一様で滑らかな分布を p として採用するという事を行っています。
( この辺の話はこちらのスライド [9] に非常に詳しく書いてあるので、良ければ参考にしてください。 )
p が満たす拘束条件とは、具体的にはクエリセットSの素性の経験分布の期待値(要はS上の各素性の平均値)と、D上の確率分布 p の期待値との絶対誤差が β_ j 以内で一致するという条件です。通常の Maxent であれば β = 0 なのですがこのように誤差を認めて緩和を許す事の意義はモデルの過学習(オーバーフィッティング)を避ける為です。以降で説明するようにこのような緩和はL1正則化と同じ効果をもたらします。
具体的に、前述の最適化問題をラグランジュの未定乗数法を使って解くと、
となり、拘束条件下でのエントロピー H(x) の最大化は、最終的にλの関数 L(λ) と | λ_ j | の線形一次結合の和、L(λ) + Σ_ j ( β_ j ・ |λ_ j | ) の最小化と等価になります。仮に β_ i = β_ j = C (i≠j) ならば L(λ) + C Σ_ j |λ_ j | となるのですが、これはいわゆるL1正則化と一致します。
学習後の識別(推定)には p(x) を使い、候補となる x すべての p(x) を計算した後、確率の高い x から順に推薦候補になります。
――― というのが教科書的な説明ですが、事前知識がないと色々難しいと思うので、以下に補足を入れておきます。
◆ <補足>
やろうとしているのは、クエリセットSを生じさせるような未知の確率分布 p を作る事が最終目的です。
この p さえ分かれば、任意のデータ X に対して p(X) を計算する事で、クエリセットSに所属するという条件の元での X の発生確率( 要はSに所属する確率みたいなモノ )が分かります。この事から、元のデータセット D の p(x) x∈D をすべて計算すれば、確率が高い順にSを補完するのに相応しいデータ、つまり推薦するのに相応しいデータが分かります。
では、どういう p ならば良いのでしょうか? 方針としては拘束条件にある通り、素性の期待値を使います。
p が生成するデータ X' はSに所属しているはずなので、X' の各素性の期待値とクエリセットSの素性の期待値が同じであれば、X' は x∈S と似たようなモノが生成されている考えられます。従ってそのような p はSを生成する確率分布として中々よろしいモノな気がします。
しかしながらこの拘束条件だけを満たす確率分布は無数に存在しているため、何らかの制限を更に付け加えなければ p が一意に定まりません。この制限のつけ方にはいろいろあるのですが、その一つが p のエントロピーを最大化させる事です。
エントロピーを最大化させるには、p の事前分布を一様分布と仮定して、p をこの一様分布にできるだけ近づける事( 確率分布間の距離を測る指標にKLダイバージェンスという指標が存在するのですが、この指標の最小化 )で実現できます。そもそもなぜ一様分布に近づけるのかというと、p の(事前)分布の形が何か推測できないのであれば、拘束条件を満たした上で確率を一様に割り振ることが自然だ・・と考えるのが最大エントロピー原理だからです。とにもかくにもこの制限を加えると"最大化"というだけあって p の確率分布は一意に定まります。
ただしこれには問題があって、このように決定される p は過学習を起こしやすいという問題点が存在します。特に |S| が小さい場合には、S上の素性の経験分布は誤差を含みやすいはづなのですが、そのような誤差を含んだ拘束条件の元で p を推定しても、結果はあまり良くはならないでしょう。
このような過学習を防ぐ方法としてよく使われる手段に正則化という考え方があります。過学習を起こしたモデルは、特定のパラメータが非常に大きくなる場合がほとんどです。そこで通常の損失項 ( 今回は L(λ) )に対して、各パラメータの絶対値の線形結合 CΣ_ j | λ_j | をペナルティ項を付け加えた L(λ) + C Σ_ j |λ_ j| を最小化するという方法がとられます。
このペナルティ項の事を正則化項といい、損失項と正則化項の和を合わせて最小化する事を正則化といいます。もし仮に、過学習で p のパラメータが非常に大きな値をとっている場合では、正則化項が大きくなっているため目的関数全体として値が大きくなります。よって、そのようなパラメータは目的関数を最小化させるパラメータにはなりえません。
今回の MaxentSets では、直接的に正則化項を付け加えているわけではありませんが、前述の通り、『 S上の素性の経験分布の期待値と D上の p の期待値の差をβだけ許す 』という緩和的な拘束条件を与える事で、結果的に正則化項に相当するモノを導いています。
この正則化項のおかげで、MaxentSets はクエリセットSが少数の場合であっても、過学習を起こしづらい推薦結果を生成してくれるというわけです。ちなみに MaxentSets のより詳細な説明はこちら [10] にありますので、良かったら参照してみてください。
■ MaxentSetsの解法 - λの求め方 -
具体的な MaxentSets の λ のパラメータ推定方法ですが、これには勾配法的なやり方や、SMO的なやり方など様々な手法が存在します。一般的に maxent 周辺では準ニュートン法の一種である L-BFGS 法 [11] を使うのが主流ですが、今回のケースではL1正則化項が入っているためそれに対応した最適化法を使う必要があります。そこで今回は、L1正則化項の微分不可能点を考慮できる Orthant-wise L-BFGS [12] を使った方法で最適化を試みました。
ちなみに余談ですが、MaxentSets の論文で採用されているパラメータ推定方法は、Orthant-wise L-BFGS ではなく、L1-SUMMET ( Selective-Update algorithm for MaximuM Entropy ) [8] と呼ばれる手法です。
結論から言うと L1-SUMMET は遅くてデータ規模が大きくなると殆ど使えないのですが、L1-SUMMET は Orthant-wise L-BFGS とは異なり、理論的にパラメータ学習の収束保証が付いているという違いがあります。MaxentSets の著者らはその辺りを買って、敢えてこのやり方を採用しているみたいです。
( *ちなみにOrthant-wise L-BFGSは "理論的な" 収束保証はないのですが、実際には収束するので特に問題はありません )
■ 性能評価・推薦結果
Ameba の実データを用いて、下記の条件で MaxentSest を用いた芸能人推薦の結果を作成してみました。また比較のために BayesianSets の推薦結果も併記しておきます。
【データ】 : ブログのユーザーのアクセスログ1週間分
【素性】 : 共起アクセスされた芸能人 (作成方法は既出スライドを参照)
データmatrixの軸は 芸能人×芸能人で、一辺は 約8000
【推薦方法】 : BayesianSets、MaxentSets ( Orthant wise L-BFGS [収束半径:10^-2] )
【環境】 : OS : Winows7(64bit)、CPU : Core i7-2620M、2.7GHz、 メモリ : 8G
【実装言語】 : Java
【クエリ】 : tanaka-masahiro、moemode、takigawa-christel、osamu-labo

結果は上記のとおりです。各カラムの左側が MaxentSets の結果、右側が BayesianSets の結果です。また各カラムの右上に表記してある数字が推薦結果を作成するためにかかった時間(ms)で、写真の隣の id は芸能人のamebaID、そしてカラムは上から順により推薦すべき候補が並んでいます。
各推薦結果の上位を見ると共に似通ってはいるのですが、推薦の下位になってくると多少違う芸能人が推薦されており、ちょっとした多様性が入っている感じです。どちらの方が精度がいいのか?というのは人の感性や推薦された時期によって異なるので、なんとも言えないのですが、variation があるのはいい事ではないでしょうか?
一方性能面(計算速度)を見ると、芸能人約8000人の候補からデータから推薦結果を作成するのに MaxentSets では1秒後半~3秒程度の時間がかかる一方で、BayesianSetsは 100ms 以下しかかかりません。
このように BayesianSets が速度で圧勝する理由は、BayesianSets の場合 MaxentSets でいう所の p の推定をする必要がないためです。実際上記で示した MaxentSets の推薦にかかる時間のうち 99% 以上はλのパラメータ推定にかかる時間です。
MaxentSets の推薦時間は、パラメータ推定のアルゴリズムの計算オーダーに引っ張られます。今回は準ニュートン法を使用しているのですが、データセットが大規模になり、素性が増えていくと計算結果はどんどん遅くなっていきます。今回のケースの規模ではバッチ処理前提であれば、マルチコアCPUを使って推薦結果を数時間で作れるので特に問題はないですが、データ規模(素性の数)が 10^5 を超えてきたら MaxentSets を実用的に使うのはちょっときついかな…というイメージがあります。
■ 雑記・感想など
今回 "On-demand" Sets-based Recommendations という論文のフレーズに釣られて、論文を読み進めたのですが、実際やってみるとそこまで On-demand でもない事に気づかされてがっかりしたのですが、同じデータセットから別の推薦結果を得られるのは色々と便利です。
というのは、この手の推薦では特定のアルゴリズムを使用していると、多様性の問題もさる事ながら、アルゴリズムの特性で推薦上位に、しばしよく分からない結果が入ってくるケースがあるからです。
多様性と割り切って気にしないというのも手ですが、別のアルゴリズムを使うとその誤差が混入しないというのは、割とあるというのが実感です。一方で本質的に推薦されるべきもの?はどのアルゴリズムを使っても推薦の上位に入ってくるので、うまく推薦結果を組み合わせたり、結果の出しわけをすると誤差を避けられるかもしれません。
( データが濃いところは何を使っても良い結果が出る一方で、データの薄い所の特徴ほど、アルゴリズムの手法によって左右されるという話なんだと思います。 )
実際にサービス化とかを考えた場合、推薦モジュールに表示される推薦の数は決して多くはなく(特にモバイルでは)、微妙な結果を出すとユーザーも微妙に感じてしまいます。
という訳で、やっぱりいろんな持ち駒があるといいよね?という感じにまとめて今回は終了したいと思います。長々と最後までおつきあい頂きましてありがとうございました。
■ Reference
[1] Google Sets
[2] Boo!Wa!
[3] Bhavana Dalvi、Jamie Callan、 William Cohen : Entity List Completion Using Set Expansion (2011)
[4] Brian Roark and Eugene Charniak : Noun-phrase co-occurrence statistics for senti-automatic semantic lexicon construction (1998)
[5] Michael Thelen and Ellen Rilo : A Bootstrapping Method for Learning Semantic Lexicons using Extraction Pattern Contexts (2002)
[6] Zoubin Ghahramani and Katherine A. Heller : Bayesian Sets (2005)
[7] Suhrid Balakrishnan : On-demand set-based recommendations (2010)
[8] Miroslav Dudik、Steven J.Phillips、Robert E.Schapire : Maximum Entropy Density Estimation with Generalized Regularization and an Application to Species Distribution Modeling (2007)
[9] 岡野原大輔 : 最大エントロピーモデル周辺の話 (2007)
[10] Miroslav Dudik、Steven J.Phillips、Robert E.Schapire : Performance Guarantee for Regularized Maximum Entropy Density Estimation (2004)
[11] DC Liu : ON THE LIMITED MEMORY BFGS METHOD FOR LARGE SCALE OPTIMIZATION (1989)
[12] G Andrew、J Gao : Scalable Training of L1-Regularized Log-Linear Models (2007)