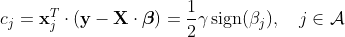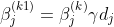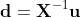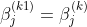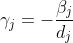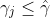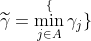Lasso-Lars その４ larsアルゴリズムのlasso modification

こちらに書いたようにlasso解は、βj と残差 v.s. xj との相関 cj の符号が

式（１）


と等しくなる事が課せられます。しかし Lars アルゴリズムそのままではこの条件は必ずしも満たされません。
例えば今 k 回目のステップの解 が式（１）を満たす lasso 解であるとします。
次の k+1 回目のステップで、新たな等角方向 u に推定値 μ を動かします。



これにより βj は

式（２）


と変更されます。ここで



です。

式（２）で重要なのは、γ=0 のとき



で lasso 解、つまり式（１）を満たすという事です。式（２）から

式（３）


の時 βj =0 となるので

１． γj < 0 ならγj < γ で、
２． 0 < γj なら γ < γj で βj は符号が変わらないので式（１）を満たす

という訳です。

今は γ > 0 としているので ２．の場合のみを考えれば、前回の記事のEfron論文の式（２．１３）で求められた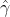 が



なら βj の符号が変わるので式（１）が満たされず、lars の解ではあっても lasso 解では無くなります。

このような状況が最初にあらわれるのは、γの値が



になったときです。この時 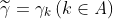なら最初に βk が0になり lasso解で無くなります。

こうした事を回避するため larsアルゴリズムに以下のような修正を施します。

となったら とする、つまり βk = 0 として　ｘk をアクティブセット A （βが0でない指標の集合）から外し、改めて xk を抜いて等角ベクトルを求めなおす。

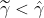
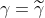
以上の修正を施す事で lasso 解を larsアルゴリズムで求められます。