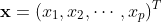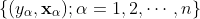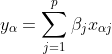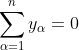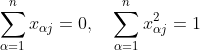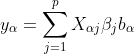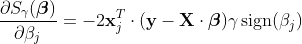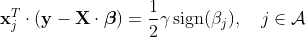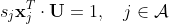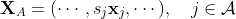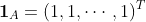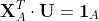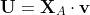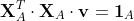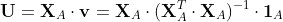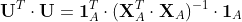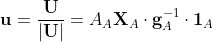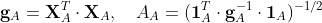Lasso-Lars その１ | ぽんのブログ

ホームピグアメブロ

芸能人ブログ人気ブログ

ぽんのブログ

自分用の備忘録ブログです。書いてある内容、とくにソースは、後で自分で要点が分かるよう、かなり簡略化してます（というか、いい加減）。あまり信用しないように（汗

Lasso-Lars その１

最近 Lasso-Lars というL1正則化推定法が注目されているそうです。
この方法ではパラメータ推定と共に説明変数の選択も同時に行う事が出来るそうです。

その説明と使用例についてはこちらなど・・・

本ブログでは Efron et al. さんの論文に則ってその具体的な計算方法をまとめたいと思います（興味が続けばですが・・・汗）

今、目的変数Yと p 次元の説明変数

${\bf x}=(x_1,x_2,\cdots,x_p)^T$

に関して、n組のデータ

$\{(y_{\alpha},{\bf x}_{\alpha}); \alpha=1,2,\cdots,n\}$

が観測されたとします。

これから以下の様な線形の式

式（１）
$y_{\alpha}=\sum_{j=1}^p \beta_j x_{\alpha j}$

で回帰する事を考えます。

普通の最小二乗で解く場合には、観測データと式（１）の推定値との残差二乗

$s(\boldsymbol{\beta})=({\bf y}-{\bf X}\cdot\boldsymbol{\beta})^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})$

を最小にするのですが、Lassoでは上に加え

式（２）
$S_{\gamma}(\boldsymbol{\beta})=({\bf y}-{\bf X}\cdot\boldsymbol{\beta})^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})+\gamma\sum_{j=1}^p|\beta_j|$
と、βの絶対値の和、つまりL1ノルム制約を課したものを最小化します。
但しLassoでは

$\sum_{\alpha=1}^n y_{\alpha}=0$

と y について中心化、

$\sum_{\alpha=1}^n x_{\alpha j}=0, \quad \sum_{\alpha=1}^n x^2_{\alpha j}=1$

と x について基準化してあるものとします。

中心化していない場合式（１）は

$y_{\alpha}=\sum_{j=1}^pX_{\alpha j}\beta_j+b_{\alpha}$

と、切片 b を考えなければなりません。
さらに X の各列、即ち各々の説明変数がスケーリングされて同じノルムを持っていない場合、βからデータへの寄与率をそのまま測る事ができません。例えばβが全て同じ値でも、説明変数のノルムが10のものと1のものではデータへの寄与は同ではありません。
或いは、ノルムが飛びぬけて大きいものが含まれていたら（あるいは小さなものが含まれていたら）式（１）の回帰結果はそのノルムの大きな変数を合わせるだけで終わってしまいます（ノルムの小さいものは無視されてしまう）。

ところで、このL1ノルムの制約を加えた事で何が変わってくるのでしょう？

式（２）を 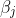$\beta_j$ で微分すると

$\frac{\partial S_{\gamma}(\boldsymbol{\beta})}{\partial \beta_j}=-2{\bf x}_j^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})\gamma\, {\rm sign}(\beta_j)$

となります。

これを0にするもの、つまり式（２）を最小にする 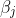$\beta_j$ 　は

式（３）
${\bf x}_j^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})=\frac{1}{2}\gamma\, {\rm sign}(\beta_j), \quad j\in {\cal A}$

となります。
これはつまり、観測データとLasso推定値との残差が、全ての目的変数 x についてその内積（の絶対値）が等しい、つまりそれぞれの成す角が等しい事を表します。

Larsというアルゴリズムでは、式（３）が満たされるよう、順次説明変数を増やしながら予測値を動かす事を行います。

まず y との相関が最も高い説明変数を採用し、その添え字を 1 とします。
予測値 μ の初期値は 0 とし、それを最小二乗解の方向に移動します。
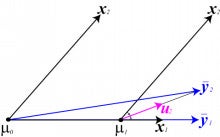
今の場合最小二乗解は、 y を x1 軸に投影した y1 です。

すると　μ1 のところで、x1 - x2 平面上の最小二乗解との残差 (y2 - μ1) と x1 及び x2 との相関が等しくなります。

$|{\bf x}_1^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})|=|{\bf x}_2^T\cdot({\bf y}-{\bf X}\cdot\boldsymbol{\beta})|$

ここで今度は上の式を満たしながら最小二乗解 y2 に向け予測値を移動させます。
上の式を満たす方向は、x1 と x2 の成す角を等分する上の図の u の方向になります。
これにより β2 も0でない値をとります。

このようにLarsでは、順次説明変数を加えながら、解をそれら説明変数と等角となる方向に修正してゆきます。
また、採用された説明変数の（βが0でない）添え字集合 A をアクティブセットと呼びます。

ところでこの解を修正するべき方向、つまり全ての目的変数 x との内積が等しい方向 u はどうやって求めるのでしょう？

今その方向のベクトルを U とし、Aに含まれる任意の x との内積が 1 となるとします。

式（４）
$s_j{\bf x}_j^T\cdot{\bf U}=1,\quad j\in{\cal A}$

ここで s_j は sign (β_j) の符号を表します。

ここで

${\bf X}_A=(\cdots,s_j{\bf x}_j,\cdots),\quad j\in{\cal A}$

を A に属する説明変数の列ベクトルを横に並べた行列、

${\bf 1}_A=(1,1,\cdots,1)^T$

を、式（４）の右辺の 1 をAに属する説明変数の数だけ縦に並べたもの
（ octaveで書けば ones (length(A), 1) ）
とすれば、式（４）は、Aに属する全ての x を用いて

式（５）
${\bf X}_A^T\cdot{\bf U}={\bf 1}_A$

と表されます。ここで新たに

${\bf U}={\bf X}_A\cdot{\bf v}$

なるベクトルを導入すれば式（５）は

${\bf X}_A^T\cdot{\bf X}_A\cdot{\bf v}={\bf 1}_A$

即ち

${\bf U}={\bf X}_A\cdot{\bf v}={\bf X}_A\cdot({\bf X}_A^T\cdot{\bf X}_A)^{-1}\cdot{\bf 1}_A$

が得られます。さらに

${\bf U}^T\cdot{\bf U}={\bf 1}_A^T\cdot({\bf X}_A^T\cdot{\bf X}_A)^{-1}\cdot{\bf 1}_A$

なので式（５）を満たす方向の単位ベクトル u は

${\bf u}=\frac{{\bf U}}{|{\bf U}|}=A_A{\bf X}_A\cdot{\bf g}_A^{-1}\cdot{\bf 1}_A$

${\bf g}_A={\bf X}_A^T\cdot{\bf X}_A,\quad A_A=({\bf 1}_A^T\cdot{\bf g}_A^{-1}\cdot{\bf 1}_A)^{-1/2}$

となり、Efronさんの論文の式（２．６）の equiangular vector が導かれます。