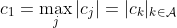Lasso-Larsによる回帰がどう行われるのか、もうすこし例を用いて概説します。
今一次独立なベクトル(説明変数) x1、x2、x3 を考え、これにより観測データ y を説明する事を考えます。ここで観測値 y の x1-x2 が張る面への投影を y2 、x1-x3 が張る平面への投影を y3 とします。
3つのベクトルが張るのは面じゃなく空間になりますが、3次元の図示は難しいので、そのさらにある平面への投影が上の図だと思ってください。
1.解の推定値 μ について、初期値として 0 を与える(μ0)。
このとき説明変数は一つも選択されていないのでアクティブセット A は空です。
2.説明変数のうち最も y と相関の高い(yとの内積の値が大きい)ものを選択しアクティブセットに加える。
上図の場合だと x1が選択されます。
3.μを x1 方向に移動させる。
つまり
とします。
4.
を満たす最小のγを選び、それに対応する j をアクティブセットに加える。
γを少しずつ大きくしてゆくと、上の図の場合 γ=γ2 のとき残差 (y - μ1) と x1 及び x2 の相関が等しくなります( u2 が x1 と x2 の成す角を二等分する)。
さらにγ=γ3 のとき残差 (y - μ1') と x1 及び x3 の相関が等しくなります( u3 が x1 と x3 の成す角を二等分する)。
これらのうち最も相関の高いものを選択します。
上の図の場合、(y-μ1)のほうが(y-μ1')より x1 と成す角が小さい、つまり相関(内積)が大きいので γ として γ2 を選びます。これは上の条件を満たすより小さい γ を選ぶ事に相当します。
5.新たなアクティブセットから等角ベクトル u を前回の記事の計算式で求めその方向に μ を修正する。
あとはこの繰り返し。
上の手順で解の推定値 μ を求めてゆくと、アクティブセットに含まれる説明変数と残差
(y - μ) の相関は、全て等しく最大値を取ります。
つまり
「アクティブセットに含まれる説明変数と残差の相関は最大」
「アクティブセットに含まれる変数と残差の相関は全て同じ値」
が成り立ちます。
残差と説明変数の相関の値についてですが、上の1.の μ0 = 0 の場合
となります。1.で書いたように全ての x のうちで x1 は y と相関が最も高い訳ですから
と c1 が全ての説明変数の、この時点での残差に対する相関の最大値になります。
2.でこの x1 がアクティブセットに加えられたので
式(1)
つまり「アクティブセットに含まれる説明変数と残差の相関が最大」が成り立ちます。
次に3.の手順の様に μ を動かしてゆくと
となって、γを0からだんだん大きくするに従い、相関の値は単調に小さくなります。
ただ、γを大きくしていっても、最初のうちは x1 と残差の相関は全説明変数中最大のままですが 4.の γ=γ2 の段階で残差との相関は x2 のそれと同じ値になります。
4.で x2 も A に加えられるので「アクティブセットに含まれる変数と残差の相関が最大」は依然として成り立ち、かつ
なので「アクティブセットに含まれる変数と残差の相関は全て同じ値」が成り立ちます。しかも5.では x1 と x2 の相関が同じ値になる u2 (等分角ベクトル)上を移動するので5.でもこれは満たされます。
3.の時と同様、5.で u2 方向に μ を変更してゆくと残差との相関は単調に減少し、やがて x3 と相関が同じ値(4.の状況)になります。そこで x3 もアクティブセットに加え x1、x2、x3 の等分角ベクトルを求め、最後に μ は y の最小二乗解 (y の x1、x2、x3 が張る空間への投影)に一致します。
変数の数が 3 個以上あれば、4.と5.をアクティブセットに入っていない残りの変数の回数分だけ繰り返します。