GSL線形代数ルーチン読解: ハウスホルダー変換（１）

ハウスホルダー (Householder) 変換とは、長さ（ノルム）の等しい二つのベクトル x、y について
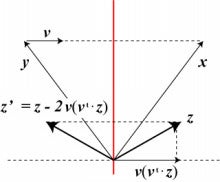
y にこの変換を施すと x に、x に施すと y になるような直交変換のひとつです。

ここで、ベクトル x、y を共に長さの等しい列ベクトル

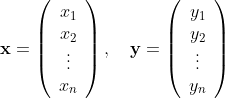
${\bf x}=\left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right),\quad {\bf y}=\left( \begin{array}{c} y_1\\ y_2\\ \vdots\\ y_n \end{array} \right)$

とします。
で、ハウスホルダー変換は、具体的には以下の直交行列で表されます。

式（１）
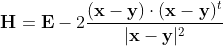
${\bf H}={\bf E}-2\frac{({\bf x}-{\bf y})\cdot({\bf x}-{\bf y})^t}{|{\bf x}-{\bf y}|^2}$

ここで E はn次の単位行列、右辺第二項の分子の部分は、列ベクトルとその転置の積なので

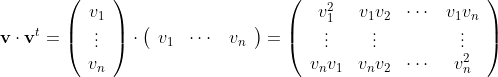
${\bf v}\cdot{\bf v}^t=\left( \begin{array}{c} v_1\\ \vdots\\ v_n \end{array} \right)\cdot \left( \begin{array}{ccc} v_1 & \cdots & v_n \end{array} \right)= \left( \begin{array}{cccc} v_1^2 & v_1 v_2 & \cdots & v_1 v_n\\ \vdots & \vdots & & \vdots\\ v_n v_1 & v_n v_2 & \cdots &v_n^2 \end{array} \right)$

という対称な行列になります。
これは、右から列ベクトルを掛ければ 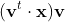$({\bf v}^t\cdot{\bf x}){\bf v}$ という長さの列ベクトルを返す（左から行ベクトルを掛ければ行ベクトルを返す）演算子みたいなものだと考えればいいのでしょうか？

上の行列 H で x を変換してみると

式（２）
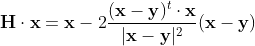
${\bf H}\cdot{\bf x}={\bf x}-2\frac{({\bf x}-{\bf y})^t\cdot{\bf x}}{|{\bf x}-{\bf y}|^2}({\bf x}-{\bf y})$

ここで

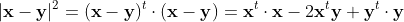
$|{\bf x}-{\bf y}|^2=({\bf x}-{\bf y})^t\cdot({\bf x}-{\bf y})={\bf x}^t\cdot{\bf x}-2{\bf x}^t{\bf y}+{\bf y}^t\cdot{\bf y}$

x と y は長さが同じなので

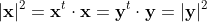
$|{\bf x}|^2={\bf x}^t\cdot{\bf x}={\bf y}^t\cdot{\bf y}=|{\bf y}|^2$

が成り立ち、従って上の式は

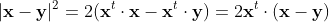
$|{\bf x}-{\bf y}|^2=2({\bf x}^t\cdot{\bf x}-{\bf x}^t\cdot{\bf y})=2{\bf x}^t\cdot({\bf x}-{\bf y})$

ここで x^t (x - y) はベクトル x と (x - y) の内積なので、当然 (x - y)^t x と同じ値になるので

式（３）
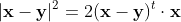
$|{\bf x}-{\bf y}|^2=2({\bf x}-{\bf y})^t\cdot{\bf x}$

これを式（２）に代入すれば

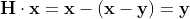
${\bf H}\cdot{\bf x}={\bf x}-({\bf x}-{\bf y})={\bf y}$

が成り立ち、確かに H により x が y に写される事が分かります（ y → x も同様）。

ここで式（３）ですが、２次元（萌え）の場合でこの式の意味を考えてみます。

この図で見ると、ベクトル (x - y) の長さは、 (x - y) と x の成す角を α として

式（４）
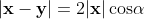
$|{\bf x}-{\bf y}|=2|{\bf x}|\, \mathrm{cos}\alpha$

となる事が分かります。式（３）は単にこの事を言っているにすぎません。
実際、| x | cos α は、 (x - y) 方向の単位ベクトルを v として

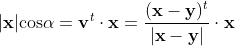
$|{\bf x}|\mathrm{cos}\alpha={\bf v}^t\cdot{\bf x}=\frac{({\bf x}-{\bf y})^t}{|{\bf x}-{\bf y}|}\cdot{\bf x}$

となり、式（４）から式（３）が導かれる事が分かります。

以上から、ベクトル x - y は

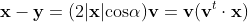
${\bf x}-{\bf y}=(2|{\bf x}|\mathrm{cos}\alpha){\bf v}={\bf v}({\bf v}^t\cdot{\bf x})$

となるので

式（５）
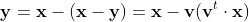
${\bf y}={\bf x}-({\bf x}-{\bf y})={\bf x}-{\bf v}({\bf v}^t\cdot{\bf x})$

が導かれます。
長さの等しい（ついでに、向きの異なる）2つのベクトルがあれば、それらの終点を結んで出来る三角形は上の図のような2等辺三角形になり、x と y は2等辺三角形の頂点から底辺へ下ろした垂線（上の図の赤線）に対し鏡映（像？）の関係になります。そのため式（３）が成り立ち、且つ式（１）で x → y、y → x と写される訳です。

この x → y、y → x の変換自体を表す行列は、式（５）の右辺を x でくくった式（１）になります。
x に式（１）の行列 H を作用させれば y に写されますし、 x 以外の任意のベクトルを作用させれば x → y と同じ規則で、つまり x と y で決まる赤線に対し鏡映の位置にあるベクトルへと写されます。

ここまでは2次元で話を進めてきましたが、3次元やそれ以上でも、2次元の場合の垂線（赤線）に当たる物（ν を法線に持つ超平面）に対する鏡映に写されるため、Householder変換を鏡映変換とも呼ぶようです。

ここらへんの話は、有名有用な物理のカギのしっぽ様とか数理ファイナンス様などを参照されればもっと良く分かると思います（まるなげ）。

図はしっぽっぽ様とほとんど同じだし（汗

ぽんのブログ

自分用の備忘録ブログです。書いてある内容、とくにソースは、後で自分で要点が分かるよう、かなり簡略化してます（というか、いい加減）。あまり信用しないように（汗

GSL線形代数ルーチン読解: ハウスホルダー変換（１）