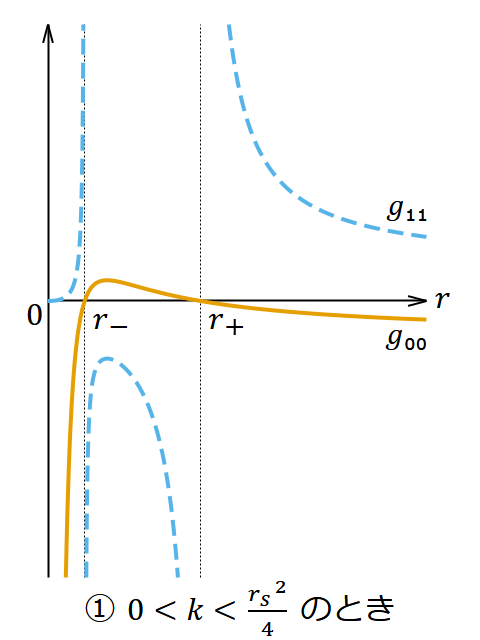
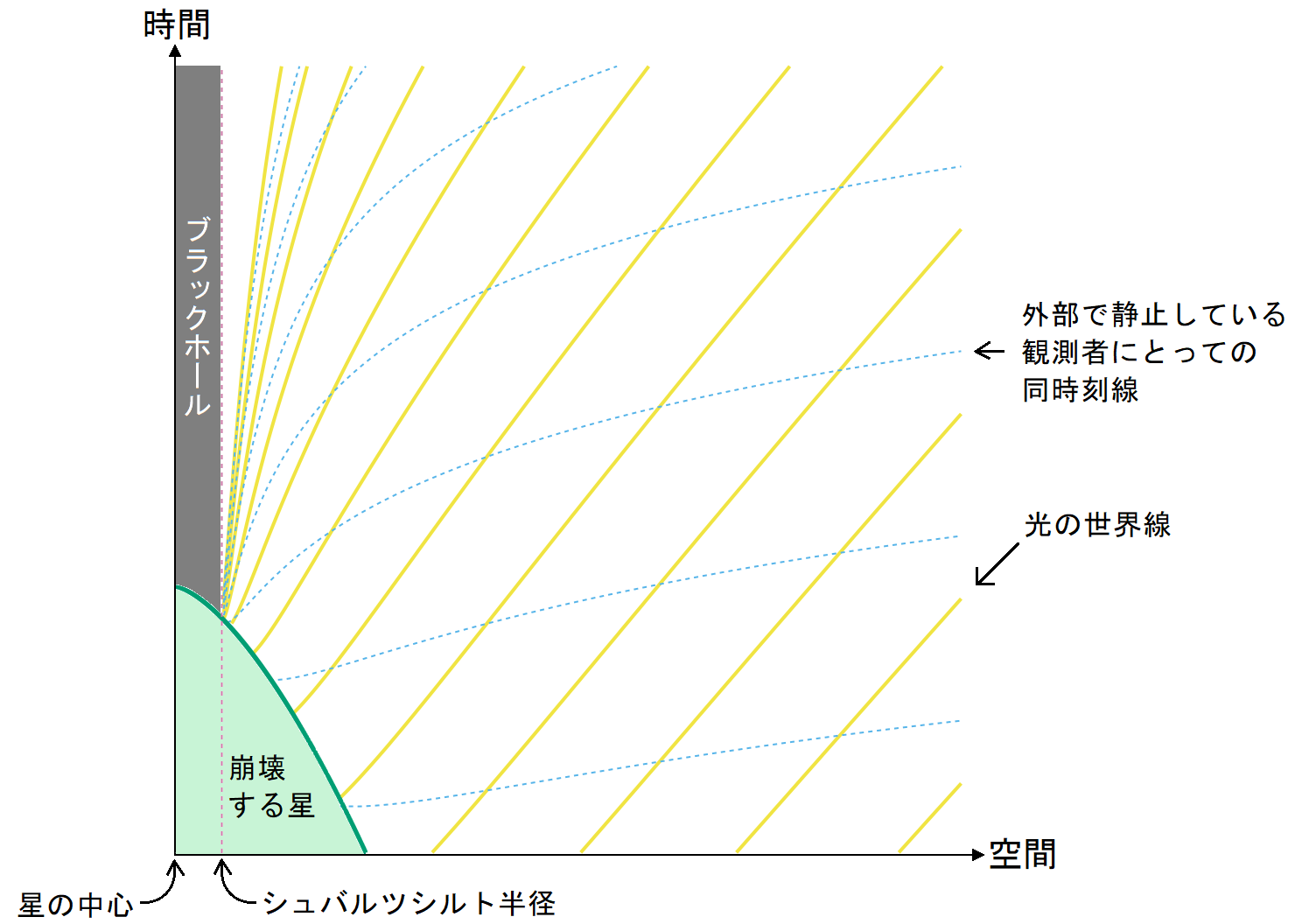
ライスナー・ノルドシュトルム解は、電荷があって角運動量が0のブラックホールの解、あるいは電荷があって角運動量が0の球対称の物体の外部の真空の解である。
計算方法や表記を工夫することで少ない計算量や少ない文字数で解を導出する方法がいろいろ提案されているが、それらが必須なわけではない。下のページではただ普通にアインシュタイン方程式を式変形するだけの単純なわかりやすい方法で解を導出する。
この解の名称は Hans Reissner さんと Gunnar Nordström さんに由来している。
最初 Nordström さんってドイツの北川さんかと思ったけど、ドイツでなくフィンランドの人のようだ。細かいことを言えばドイツ語で「川」は Strom (単数), Ströme (複数)だから仮にドイツ語だとしても北川さんとはちょっと違うのかもしれないが。Google翻訳に入れたらスウェーデン語で“Nord ström”が「北大西洋海流」と出てきた。
この人の名前の片仮名表記は「ノルドシュトルム」の他に「ノルドシュトロム」とか「ノルドストローム」とかいろいろ見かける。どう書くべきかなんてひとつに決められないがそれは別として、現地での発音はどう聞こえるのだろう。特に「s」とか「ö」の辺り、フィンランドではどうなの?
私はフィンランド語をまったく知らないが、 Wikipedia 日本語版の「フィンランド語」や「フィンランド語アルファベット」によると s は /s/ で ö は /ø/ と読むのが普通っぽい。 Forvo の「Gunnar Nordström」を聞くと、やはりなんとなくそのように言っている気がする。しかし特に固有名詞は一般論が当てはまるとは限らないし、フィンランド人の名前だからと言ってフィンランド語で読むのが正しいとも断言できない(例えば、スウェーデン語かもしれない)ので、何とも言えない。
「シュ」と書くのはドイツ語なまりなのだろうか。ドイツ語だったら ö (/œ/, /øː/) はたいてい「エ」(の段)で書かれると思う。例えば、山から熱気が降りてくる Föhn 現象とか、橋が7つあった Königsberg 市とか、高温超伝導の Schön さん等。フランス語の /ø/ だとまた違って、「ウ」(の段)で書かれることが多いのではないかな(よく知らんけど)。言語によって多少の差異はあっても、強いて言えば /ø/ はだいたい「ウ」と「エ」の間ぐらいの音に聞こえて「オ」はちょっと遠いのではないだろうか。
「ライスナー‐ノルドストリョームの解」という変わった表記例も見つかる。 Goethe /ˈɡøːtə/ を「ギョーテ」と書くのと同じようなものだろう。 Nordström はロシア語で Нордстрём と表記するらしいのでロシア語で読んだのかもしれない(ロシア語の ё は /jo/)。
「ライシュナー・ノルドシュトローム解」と書いている文献もあって、 Nordström さんの「s」だけでなく Reissner さんの「ss」まで「シュ」になっている。信念をもってそう書いているのだろうか。