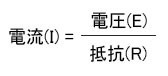オームの法則とキルヒホッフの法則の問題

必要な根本知識は、

　　オームの法則とキルヒホッフの法則

オームの法則は、電気に携わる者として、知って当然の知識ですね。

電流は、電圧に比例し、抵抗に反比例する。

これが、オームの法則です。

これを式にすると 

 

これを変形して電圧を求める式にすると

電圧(E) = 電流(I)・抵抗(R)

抵抗器に流れれば、抵抗器の両端に電圧が生じるということです。

キルヒホッフの第二法則では、

「電気回路に任意の閉路をとり電圧の向きを一方向に取ったとき、閉路に沿った各素子の電圧 V_i の総和は 0 である。」
 

判りにくいですよね。

出題された回路の場合に当てはめて、解りやすく言えば、

「抵抗器に電流が流れて生じた電圧の総和は、加えた電圧に等しい。」

ということです。

出題された回路のb-c-c'-b'間を見ると、電圧は、b-b'間の負荷抵抗に流れて生じた電圧とみなすことができるます。

b-b'間の電圧をV_bb'するとし、b-c-c'-b'の回路上の各抵抗で生じる電圧をV_bc、V_cc',V_c'b'とします。

流れている電流をI_bCC'b'とします。

キルヒホッフの法則の第二法則に従って、式に表すとb-b'間の電圧は

V_bb'=　V_bc + V_cc' + V_c'b

出題された問題でわかっている値は、

I_bCC'b = 10A

V_cc' =100V

r=0.1Ω

b-c間のrの抵抗0.1Ωにも、c-'b'間のrの抵抗0.1Ωにも電流は、10A流れます。
オームの法則により

V_bc= I_bCC'b x r =10[A] x 0.1[Ω]　= 1[V]

V_c'b'は、c-'b'間のrに流れる電流値も、抵抗値もとV_bcと同じなので1[V]です。

b-b'間の電圧は、

V_bb'=　V_bc + V_cc' + V_c'b= 1[V] + 100[V] + 1[V] = 102[V]

同様にa-b間とa'-b'間のそれぞれの電圧がわかればa-a'間の電圧が求められます。

a'-b'間とa-b'間の電流がわからないと計算できませんね。

キルヒホッフの第一法則というものがあります。

「電気回路の任意の節点において、流れ込む向きを正（又は負）と統一するとき、各線の電流 I_iの総和は0となる。」

これもわかりづらいですね。

問題中の回路で言うとb点やb'点では、線が分岐しています。

b点やb'点では、電流が、いずれかの線から流れ込み、いずれかの線から流れ出ます。

「この時の流入する電流の総和と流出する電流の総和の値は等しい」

ということです。

つまり、出題された回路で具体的に言うと、b点では、b'点の方に流れて出いく電流は5A、c点の方に流れ出ていく電流は10Aです。

b点に入り込んでくる電流値は出て行く電流値等しくなければなりませんから、とa点からb点に入り込んでくる電流は、

　5[A] + 10[A] =15[A]　・・・　a-b間の電流

b'点では、b点から入り込んでくる電流は5A、c'点の方に流れ込んでくる電流は10Aです。

b'点からa'点に流れて出いく電流は、

5[A] + 10[A] =15[A]　・・・　a'-b'間の電流

a-b間、a'-b'間の抵抗値も電流値も同じなので、それぞれの抵抗で生じる電圧をV_ab、Va'b'すると

オームの法則によりV_ab =　15[A] x 0.1[Ω]　= 1.5[V]

_Va'b'も同じ1.5[V]です。

従って、a-a'間の電圧は、

V_ab+　V_bb'+　V_a'b'=　1.5[V] + 102[V] + 1.5[V] = 105[V]

答え　105[V]

//////////////////////////////////////////////////////////
第二種電気工事士試験対策無料webセミナー
「マル秘　８つの合格に必要な知識」
今年(平成２７年)の後期試験は、10月３日です。今からなら、まだ、間に合います。
電気工事士は資格が無いとつけない職業です。
また、電気がある限り、無くならない職業です。
あなたが資格をもっていれば、職場でも必要とされる人材と
なれます。
収入アップも期待ですます。
この無料セミナーから、始めてみませんか？
http://dk.janets.jp/