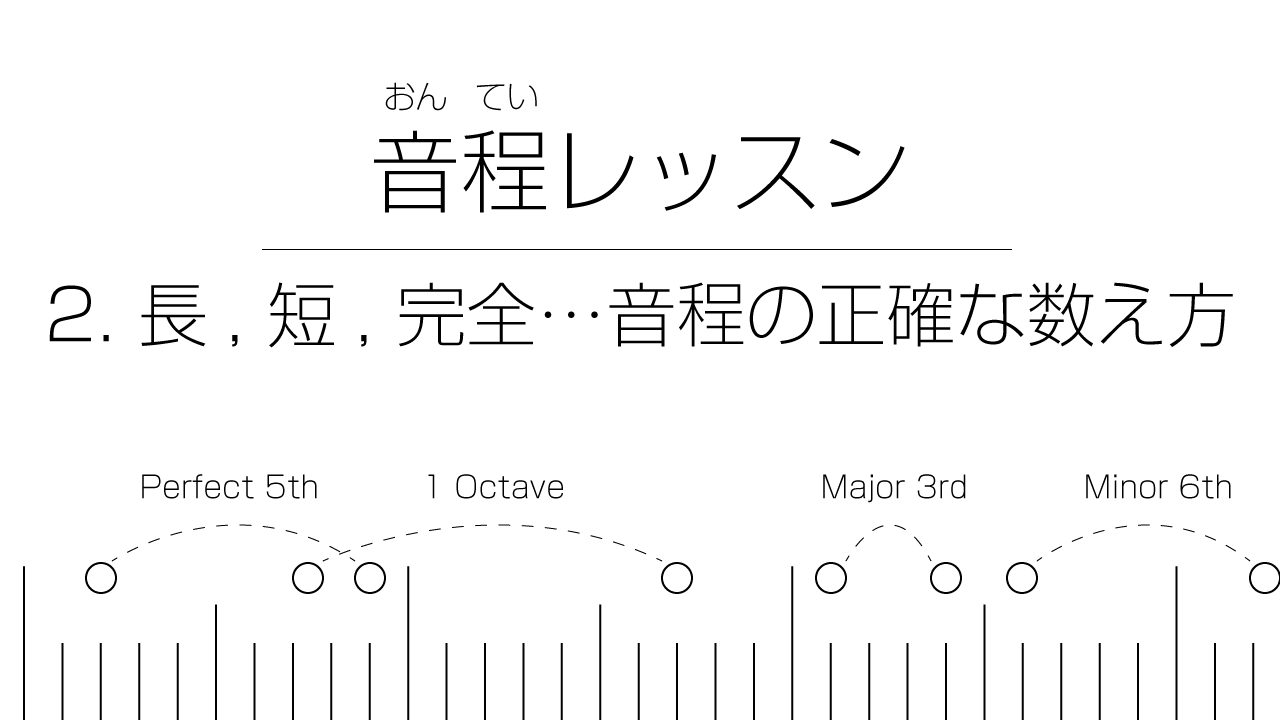
音程は何度離れているという言い方(音階上でいくつ離れているか)をする。
西洋の音楽理論では音程を現すには以下の呼び方がある。
ハ音とハ音の関係は1度と言う。
ハ音と二音の関係は2度と言う。
以下、同様に3度、4度、…、10度。
2音の一方、または両方に、♭♭、♭、#、##がついても音度の呼び方は変わらない。
ハ音と同じハ音の間の音は完全1度と呼ぶ。
ハ音とニ音の二つの音は全音離れているので長2度と呼ぶ。
左下のロ音とハ音の音程は低い方を基準に考えるので、半音離れているから短2度と言う。
ハ音と変ニの音は半音だけ離れているので短2度と言う。
ハ音と変ホの音程は短3度。
ハ音とホ音の音程は長3度。
ハ音とヘ音の音程は完全4度。
ハ音とト音の音程は完全5度。
ハ音と変イ音の音程は短6度。
ハ音とイ音の音程は長6度。
ハ音と変ロの関係は短7度。
ハ音とロ音の関係は長7度。
ハ音とオクターブ上の関係は完全8度。
(下の図で、鍵盤と対応させてみると理解がしやすい)
完全音程、長音程よりも広くなると増という言い方になる。
完全音程、短音程よりも狭くなると減という形容がつく。
♭ロ(低い音から取れる音を考える)と#ロは増1度。
減2度は同じ音になってしまう。
変ホの音と嬰ニの音は同じに受け取れるが、両者の機能は異なる。変の形容のついた音は下に下がろうとする音で、嬰の形容がついた音は上に上がろうとする音なので、音楽上では区別される。調律の仕方によっては両者は全く違う音になる。
私的メモ
内容を飲み込めなかったので補足サイトで。
転回音程はある音程と、その音程を構成する2つの音の上下関係をひっくり返したときに生じる音程との関係を言う。
ドとミ(長3)をミとド(短6)に書くと、この二つは転回音程にあるという。
ドとファ(完全4)をファとド(完全5)に書くと、完全4度と完全5度は転回音程にあるという。
転回音程の特徴の一つは、足すと完全8度の音程が得られることがある。
次は音程と周波数比の問題。
元の周波数の2倍の周波数の音は元の音の1オクターブ上の音が得られる。したがって純正完全8度の音程は2:1の数比で表わすことができる。
ある音の周波数比を2倍にすると純正完全8度の音程を得られる。これは2:1の周波数比になる。純正と形容されるのは、非常にきれいな完全8度の音程が得られるからである。
周波数比を3:2にすると純正完全5度の音程が得られる。
同様に周波数比を4:3にすると純正完全4度の音程が得られる。
周波数比を5:4にすると純正長3度の音程が得られる。
周波数比を6:5にすると純正短3度の音程が得られる。
協和をなす音程は、単純な整数比に還元できる。
古代中国では、この原理に基づいて三分損益法が考案された。
宮(きゅう)
徵(ち)
商(しょう)
角(かく)
羽(う)
変徵(へんち)
変宮(へんきゅう)
■宮の音の周波数をニ分の三倍して(宮の音の弦の長さを三分のニにカットする)徵が得られる(宮の出す音の弦の長さを三分の一を引く)。
■徵の音にその弦の長さの三分の一を加える(徵の音に対して周波数比、四分の三倍)と商が得られる。
■商の周波数比をニ分の三倍(弦の長さを三分のニにカットして)商の音の純正完全5度上の羽の音が得られる。
■羽の音の弦の長さに三分の一の長さを加えて、周波数比を四分の三にしてやると角の音が得られる。
このような手順を繰り返して「宮」「商」「角」「徵」「羽」の五音音階が得られる。
さらにこの手順をあと2回繰り返すと「宮」「商」「角」「変徵」「徵」「羽」「変宮」の7音からなる七音音階が得られる。
弦の長さの三分の一を足したり減らしたりして、一連の音を得ていく方法になる。
同じようなことは古代ギリシャの時代にも研究されていた。そうした中で、調律に関しては、さまざまな問題があることが次第にわかってきた。協和音程を積み重ねていって、きれいな音程ばかりが得られれば問題ないのだけれど、実際には、そうはいかないことがわかった。
ピタゴラス・コンマ
ハの音から始まって、その上に、純正完全5度の音程を12回積み重ねていくと、嬰ロの音が得られる。嬰ロの音がハの音になると問題はないだが、実際にはそうはならない。元となったハの音と比較するために、嬰ロを7オクターブ下げてみると、嬰ロの音の音と元のハの周波数比は、純正完全5度を積み重ねるたびにニ分の三倍になっていくので、(3/2)^12倍の周波数を持っていることになる。それを7オクターブ下げる(1オクターブ下がるごとに1/2)ので(1/2)^7倍になる。比は1より少し大きく、531441/524288という、元のハの音にたいして嬰ロの音は少し高い周波数を持った音になってしまう。
5度圏図を示す。
ある音から出発して完全5度上の音を丸くサークルの上に書く。ハの音の上に純正完全5度を積み重ねていって、嬰ロの音が得られる。この嬰ロの音はハの音より少し高い音になってしまう。この間(ハと嬰ロの間)に誤差が生じてしまう。これを発見者と言われるピタゴラスにちなんでピタゴラス・コンマという。
もう一つの問題がある。
ある音(ここではハの音)の上に、純正完全5度の音程を4回積み重ねると、ホの音が得られる。こうして得られたホの音が、ハの音に対して純正になればいいが、そうはならない。ここで、ホの音を2オクターブ下げる。こうして得られたホの音と元のハの音との周波数比は、3/2を4回掛けるわけだから(3/2)^4、2オクターブ下げるので(1/2)^2掛けることになり、(3^4)/(2^8)=81/64という周波数比になる。しかし、ハの音に対して、純正長3度は5/4なので通分すると80/64の周波数比を持つことになる、得られたホ(81/64)の音は、ハの音に対して純正な長3度をなすホ(80/64)の音に対して違う音になってしまう。両者のホの音の差をシントニック・コンマという。こういう問題を抱えながらどうやって調律していくかというのが、古来、問題になってきた。
そういった中、西洋で古くから調律に使われてきたのが、ピタゴラス音律という調律法だった。あらゆる完全5度の音程を純正完全5度でとっていき、出てきた誤差(ピタゴラス・コンマ)を演奏上あまり使わない5度間に押し込めてしまうという調律法になる。
ハ音から出発して調律するとして純正完全5度を積み重ねていって嬰ト音まで調律し、ハ音から出発して純正完全5度低く調律して変ホまで達すし、出てきたピタゴラスコンマ(誤差)を2つの音程の中に押し込めてしまう、これがピタゴラス音律だった。
中世の間はこれで構わなかった。なぜかというと例えば、ハ音を中心とした曲の場合、ハ音とホ音の長3度の音程は汚くなるわけだけれども、中世の場合、西洋の大陸側では、もともと3度あるいはその転回音程である6度の音程は不協和音とみなされていたため汚くなっても問題がなかった。それからもうひとつ、中世の間、ハ音を中心とした曲で嬰トと変ホの間の音は使わなかった。まして、嬰トっと変ホの音を同時に使うことはなかった。したがって、西洋、中世の中では、このような調律で構わなかった。
中世のあいだは、ピタゴラス調律で構わなかった。
次のルネサンス時代に入ると、ピタゴラス調律では困った問題が起こってきた、ヨーロッパの大陸側でも、3度、その転回音程の6度の音程を協和音扱いするようになった。そうすると、ピタゴラス音律が醸し出す、長3度、あるいは短6度の汚さが、問題になってきた。これ解決する方法としては、純正律という調律法がある。
これは、ハ音を中心とした曲の場合、ハホト、トロニ、ヘイハ の和音をキレイにとるために、ハとホ、ハとト、トとロ、ニとト ハとヘ、ヘとイのあいだを純正な音程(図の右の数値)でとっていくと、ハ音を中心とした和音で、大変キレイに響く。しかし、この調律法では、ひとつ困ったことが起きてしまう。二通りの幅を持った全音が出てきてしまう。調律したものを音階順に並べると、ハとニのあいだに生まれる全音は周波数比8:9になり、ニとホのあいだに生まれる全音は周波数比9:10になってしまう。8:9の周波数比をもつ全音を大全音、9:10の周波数比をもつ全音を小全音と呼ぶ、純正律で調律すると同じ全音であっても、大全音と小全音が出てきてしまう。ヘとト、イとロのあいだは大全音だが、
トとイのあいだは小全音になってしまい、音階がガタガタになってしまう。これが純正律のひとつの弱点になってしまう。
このような問題を解決するために考案されたのが、中全音律(ミーン-トーン調律)と呼ばれるものがある。これにもいくつかのプランがあるのだが、そのうち、1/4コンマ調律法を紹介する。
ハ音から出発して、すべての完全5度の音程をミーントーンの5度、つまり純正完全5度よりもシントニック・コンマの四分の一 低い5度でとっている。そして出てきた誤差を、ここでは仮に嬰トと変ホのあいだにおさめるかたりになる。中全音律という名称は、このような操作をすると、すべての全音の音程が、大全音と小全音の中間の値をとるので、中全音律といわれる。英語のミーントーンというのも同じような問題になる。ハとホの長3度をはじめとして、すべての長3度の音程が非常にキレイな(純正な)音程になる。
こうして考えられた中全音律も欠点を抱えていて、すべてのしわ寄せを、ある5度間に押し込めてしまうので、そこにウルフの5度というものが生じてしまう。また異名音というものが生じてしまう。
全音はなれた、ふたつの音、ここではトの音とイの音のあいだには、両者から半音はなれた、嬰トと変イの二つの音がある、ところが、ピアノには、トの音とイの音のあいだに、二つの音を弾き分ける鍵盤がないので、同じキーで弾かざるを得ない、機能上は別の音でも、同一の音とみなしてしまおうというのが、異名同音という。ところがミーントーンの調律法をやっていくと、この二つの音を異なった音として、理解せざるを得なくなる。それが異名異音という現象になる。このような欠点があったため、次のバロック時代に入ると、中全音律という調律法に代わって、ヴォールテンペリーレンという調律法が、広く使われるようになった。ヴォールテンペリーレンは簡単な言い方をすると、5度の積み重ね方を工夫して、これまで紹介してきた不都合をなんとか解消しようとする調律法である。大きく分けると不等分律と完全平均律の二つがある。
左に示したヴェルクマイスターという人がいろいろ提唱した調律法、3番目のヴェルクマイスター第3調律法と言われるもの。ハとト、トとニ、ニとイ、ロと嬰ヘ、のあいだを純正完全5度よりもピタゴラス・コンマの4分の1狭い5度でとって、残りをすべて純正完全5度でとるもの。
右は、ヴァロッティ=タルティーニ調律法というもの。ヘ音から始まってロ音まで純正完全5度よりピタゴラス・コンマの6分の1狭い5度でとって、残りをすべて純正完全5度でとるもの。
こうした不等分律を含むヴォールテンペリーレンの試みの中から出てきた、もう一つの調律法は、完全平均律になる。
すべての純正完全5度の音程をピタゴラス・コンマの12分の1低い5度でいくという調律法。
不等分律を含む、さまさまなヴォールテンペリーレンの試みの中から、完全平均律というものが出てくる。完全平均律は、今日のピアノの調律に広く使われている調律法になる。
完全平均律による調律は すべての音程があまりキレイではないが、現在のピアノは、フェルトが貼られたハンマーをており、もともと音がクリアでないので、そのため、完全平均律の弱点が覆い隠されている、そうしたところから、広く使われている調律法になる。
主任講師(敬称略)
徳丸 吉彦
笠原 潔