いえ、日本人の私がびっくりした話です。
きっかけは先日Twitterで拝見したこのツイート。
小1息子が14✖️14とかの二桁のかけ算の答えを暗算でサクサク答えているので
— しおりん@ゆるりおうち英語7年目 (@shiorinenglish) November 9, 2021
気になってどうやって考えているか聞いたら
ママなんで分からないの?😤
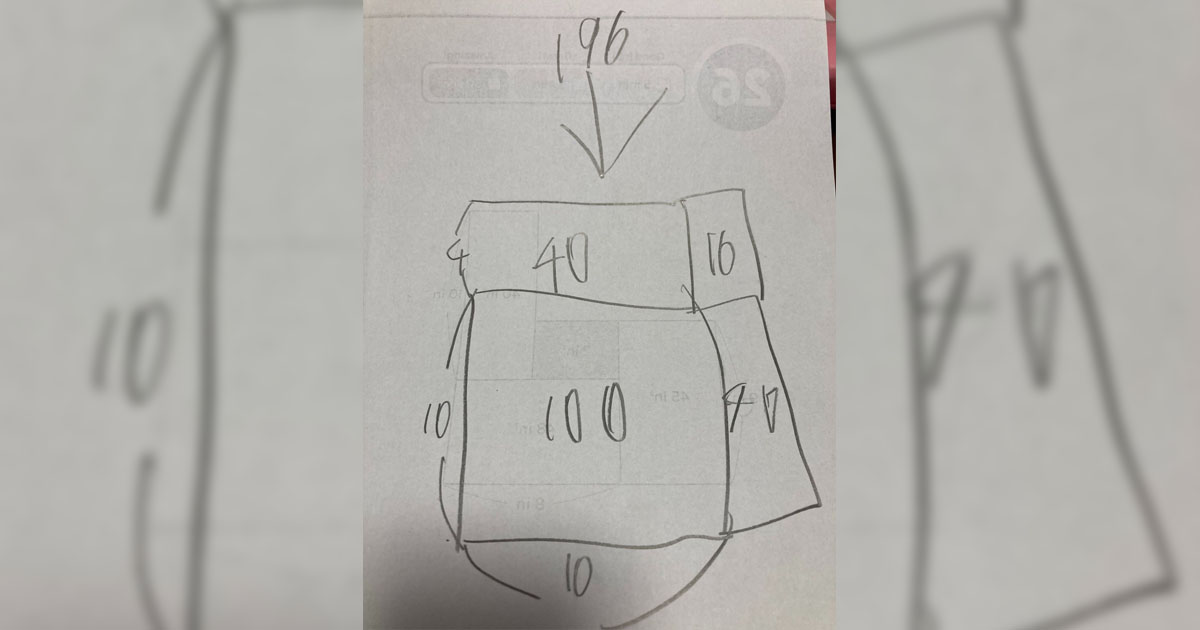
とブツブツ言いながら図解してくれました。 pic.twitter.com/W6g7alPKoM
で、Twitter上で知人とやり取りしていた際に出てきたのが「インド式計算法」の言葉でした。
さっそくGoogle大先生にお伺いしてみたところ、見つかったのがこちら。
暗算天才小学生の思考法と同じなんですね、これ。
記事の例では例題1のみ図示されているので、例題2の図をExcel方眼紙で作ってみました。
なるほどー!確かにその通りになりますね!
では17×8の場合は?というと…
上記例そのままに考えると 17+8 または 08+7 ですが、25と15になってしまい可換ではなくなります。あれ?
じゃあ17×28の場合は?
17+8 または 28+7 これも一致しません。
あるいは526×43の場合は?
526+3 または 043+6? 全然違う!
上記のパターンで計算できるのは、桁数が同じで、上位桁の数字が同じ場合、に限られるようです。
試しに思い付きで数字を書いてみますが、25×29 なら 25+9 または 5+29 でどちらも34になりますね。
前出の記事の例題というのは、インド式計算法の全てではなく、あくまで限定条件の一パターンのようです。
もう少し本質的に「インド式計算法」を知りたいと思って検索して辿り着いたのがこちらのサイト様。
ここで大事なのが「2桁×2桁の掛け算」のページに記載されていたコレ。
・全部の組み合わせを計算し、
・位を間違えずに足し合わす
これがインド式計算法の真実なのか!?と思い、前述の計算できなかったパターンについて考えてみました。
(サイト様の例に沿わず、単に上記の条件のみで考えた場合の記述です)
電卓で検算したら、ちゃんと合ってました!なるほど理解!!
国民皆スマホ(orケータイ)な昨今、これらの計算を暗算で出来る事にどれほどメリットがあるか分かりません。
というか、ほとんどないと思います。機械の方が計算早いし正確だし。
ですが。
「問題を分解して簡単にして解決する」
という思考のステップは、どんな場合でも非常に役立つのではないかと思います。
なお、冒頭のツイートの話は、ねとらぼさんでまとめられてました。