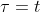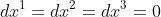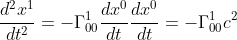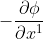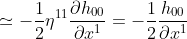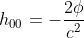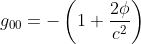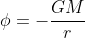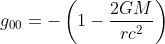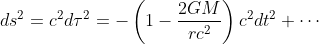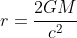今、微小四角形に沿ってあるベクトルAを平行移動させて元の地点に戻す。
簡単のため二次元を考えることにする(空間がゆがんでいるので外から見ると三次元に見えるかもしれないが)。
下図の始点をAとし、反時計回りにB,C,Dと点に名前をつける。
A→B
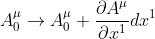
B→C

C→D
D→A
二次以上の微小項を無視して三項目、四項目をテーラー展開して計算すると
括弧内二項目、三項目をα⇔βとして
このカッコ内はリーマンテンソルや曲率テンソルといわれるものである。
平坦な空間だとこの部分は0となりベクトルAはベクトルAのままだが、空間が曲がっているとベクトルを平行移動して元に戻しても一致しないということが起こるのである。
これを導出した理由は、これを使って出てくるビアンキの恒等式と流体力学から出てくるエネルギー運動量テンソルを結び付けてやることでGとTの関係式が導出でき、これがかの有名なアインシュタイン方程式なのであるが、詳しいことは流体力学を勉強していないのでわかりかねる。
一応の帰結としてアインシュタイン方程式を載せておく
次回はシュヴァルツ解を既知のものとして物体の運動がどうなるかを軽く触れようと思う。







![=A_0^\mu+[\frac{\partial\Gamma_1 _\alpha^\mu}{\partial x^2}-\Gamma_2 _\alpha^\beta\Gamma_1 _\beta^\mu-\frac{\partial\Gamma_2 _\alpha^\mu}{\partial x^1}+\Gamma_1 _\alpha^\beta\Gamma_2 _\beta^\mu]A^\alpha dx^1dx^2](https://img-proxy.blog-video.jp/images?url=http%3A%2F%2Flatex.codecogs.com%2Fgif.latex%3F%3DA_0%5E%5Cmu%2B%5B%5Cfrac%7B%5Cpartial%5CGamma_1+_%5Calpha%5E%5Cmu%7D%7B%5Cpartial+x%5E2%7D-%5CGamma_2+_%5Calpha%5E%5Cbeta%5CGamma_1+_%5Cbeta%5E%5Cmu-%5Cfrac%7B%5Cpartial%5CGamma_2+_%5Calpha%5E%5Cmu%7D%7B%5Cpartial+x%5E1%7D%2B%5CGamma_1+_%5Calpha%5E%5Cbeta%5CGamma_2+_%5Cbeta%5E%5Cmu%5DA%5E%5Calpha+dx%5E1dx%5E2)



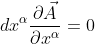
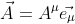
![dx^\alpha\left[\frac{\partial A^\mu}{\partial x^\alpha}\vec{e_\mu}+A^\gamma\frac{\partial \vec{e_\gamma}}{\partial x^\alpha}\vec{e^\mu}\vec{e_\mu}\right]=0](https://img-proxy.blog-video.jp/images?url=http%3A%2F%2Flatex.codecogs.com%2Fgif.latex%3Fdx%5E%5Calpha%5Cleft%5B%5Cfrac%7B%5Cpartial+A%5E%5Cmu%7D%7B%5Cpartial+x%5E%5Calpha%7D%5Cvec%7Be_%5Cmu%7D%2BA%5E%5Cgamma%5Cfrac%7B%5Cpartial+%5Cvec%7Be_%5Cgamma%7D%7D%7B%5Cpartial+x%5E%5Calpha%7D%5Cvec%7Be%5E%5Cmu%7D%5Cvec%7Be_%5Cmu%7D%5Cright%5D%3D0)