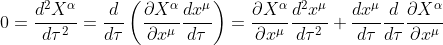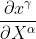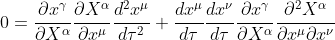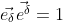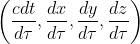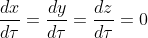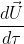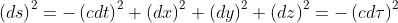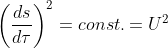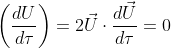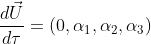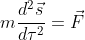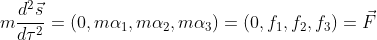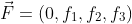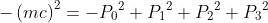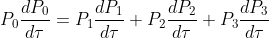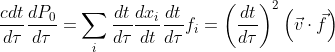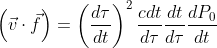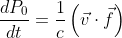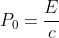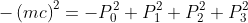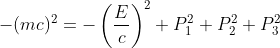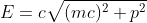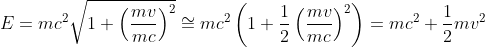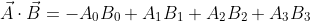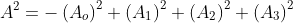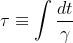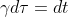バカ２匹がテンソルとか相対論とかに挑む -2ページ目

バカ２匹がテンソルとか相対論とかに挑む -2ページ目

ホームピグアメブロ

芸能人ブログ人気ブログ

第三回：メトリックテンソルｇについて

第二回は僕の担当ではないのであしからず

第三回

テーマ
$g_\mu_\nu$ とはいったいどういうものなのかをクリストエッフェル記号 $\Gamma$ の２つの定義を通して考えてみよう。

その１

局所慣性系（重力が０とみなせる系：自由落下とか）は時空が曲がってない空間とみなせることに注意する。

$0=\frac{d^2X^\alpha}{d\tau^2}=\frac{d}{d\tau}\left(\frac{ \partial X^\alpha} { \partial x^\mu}\frac{dx^\mu}{d\tau}\right )=\frac{\partial X^\alpha}{\partial x^\mu}\frac{d^2x^\mu}{d\tau^2}+\frac{dx^\mu}{d\tau}\frac{d}{d\tau}\frac{\partial X^\alpha}{\partial x^\mu}$

ここでXは局所慣性系、xは曲線座標系（曲がった空間）としている。τは固有時、μには０，１，２，３が入る。

この式の最右辺第一項の式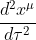 $\frac{d^2x^\mu}{d\tau^2}$ を単体で出すことができれば曲線座標系での運動方程式が導出できることになる。

そこで両辺に $\frac{\partial x^\gamma}{\partial X^\alpha}$ をかけると

$0=\frac{\partial x^\gamma}{\partial X^\alpha}\frac{\partial X^\alpha}{\partial x^\mu}\frac{d^2x^\mu}{d\tau^2}+\frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau}\frac{\partial x^\gamma}{\partial X^\alpha}\frac{\partial ^2X^\alpha}{\partial x^\mu\partial x^\nu}$

詳しい説明は省くが、右辺は次式のようになる

$=\delta_\mu^\gamma\frac{d^2x^\mu}{d\tau^2}+\frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau}\Gamma_\mu_\nu^\gamma=\frac{d^2x^\gamma}{d\tau^2}+\frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau}\Gamma_\mu_\nu^\gamma$

クリストエッフェル記号の定義二つ目

$ds^2=\eta_\alpha_\beta dX^\alpha dX^\beta=g_\mu_\nu dx^\mu dx^\nu=dx^\mu dx^\nu \vec{e_\mu}\vec{e_\nu}$

の関係より

$g_\mu_\nu=\vec{e_\mu}\vec{e_\nu}$

これを微分して

$\frac{\partial g_\mu_\nu}{\partial x^\gamma}=\frac{\partial\vec{e_\mu}}{\partial x^\gamma}\vec{e_\nu}+\vec{e_\mu}\frac{\partial\vec{e_\nu}}{\partial x^\gamma}=\frac{\vec{e_\mu}}{\partial x^\gamma}\vec{e_\nu}\vec{e_\delta}\vec{e^\delta}+\vec{e_\mu}\vec{e_\delta}\vec{e^\delta}\frac{\partial\vec{e_\nu}}{\partial x^\gamma}$

ただし $\vec{e_\delta}\vec{e^\delta}=1$ であることは認めるものとする。

$=\frac{\partial\vec{e_\mu}}{\partial x^\gamma}g_\nu_\delta\vec{e^\delta}+g_\mu_\delta\vec{e^\delta}\frac{\partial\vec{e_\mu}}{\partial x^\gamma}=\Gamma_\mu_\gamma^\delta g_\nu_\delta+\Gamma_\nu_\gamma^\delta g_\mu_\delta$

これを利用すると

$\frac{\partial g_\alpha_\beta}{\partial x^\gamma}+\frac{\partial g_\alpha_\gamma}{\partial x^\beta}-\frac{\partial g_\beta_\gamma}{\partial x^\alpha}={2\Gamma_\beta_\gamma^\delta}g_\alpha_\delta$

となることがわかる。

以上二つの関係式を使い弱い重力場について考えてみる。

尚、クリストエッフェル記号の定義式がそれぞれ違って見えるが、計算すると同じになるらしい。

第一回 -2：　相対論的運動方程式

微少の変化位置から速度の成分を求めてみると

$\left ( \frac{cdt}{d \tau },\frac{dx}{d \tau },\frac{dy}{d \tau },\frac{dz}{d \tau } \right )$

となるであろう。

ここで物体からみた座標系で観測しているので

$\frac{dx}{d \tau }=\frac{dy}{d \tau }=\frac{dz}{d \tau }=0$

また、固有時の定義式でもある

$\gamma d \tau = dt$

より、四元速度ベクトルUはこの観測では

$\vec{U}=\left ( c,0,0,0 \right )$

となる(ｖ＝０よりγ＝１)。

四次元加速度は次式であらわされる。

$\frac{d\vec{U}}{d \tau }$

ここでミンコフスキー空間において成り立つ（長さが不変）

$\left ( ds \right )^2=-\left ( cdt \right )^2+\left ( dx \right )^2+\left ( dy \right )^2+\left ( dz \right )^2=-\left ( cd \tau \right )^2$

の両辺を（ｄτ）＾２で割ると

$\left ( \frac{ds}{d \tau } \right )^2=const.=U^{2}$

となることが分かる。　この最右辺をτで微分することを考える。

$\left ( \frac{dU}{d \tau } \right )=2\vec{U}\cdot\frac{d \vec{U}}{d \tau }=0$

ここでベクトルUの成分を考慮すると、等式が成立するためには

$\frac {d \vec{U}}{d \tau }=\left (0, \alpha _{1}, \alpha_{2}, \alpha_{3} \right )$

となるであろうことが予想される。

Newtonの運動方程式はtでの微分を含んでいるので、Lorentz変換に対しては不変ではない。

なので導入した固有時間τを用いて次のようにあらわす。

$m\frac{d^2\vec{s}}{d\tau^2}=\vec{F}$

これより改めて力について考えると

$m\frac{d^2\vec{s}}{d\tau^2}=\left(0,m\alpha_1,m\alpha_2,m\alpha_3 \right)=\left(0,f_1,f_2,f_3\right)=\vec{F}$

つまり、物体からみた座標系で記述した時の力は

$\vec{F}=\left(0,f_1,f_2,f_3 \right )$

と表されることになる（物体とともに動く系なので当たり前ではあるが）。

四元運動量は次の等式が成立している（運動量をPとして）。

$-\left(mc \right )^2=-{P_0}^2+{P_1}^2+{P_2}^2+{P_3}^2$

両辺をτで微分すると

$P_0\frac{dP_0}{d\tau}=P_1\frac{dP_1}{d\tau}+P_2\frac{dP_2}{d\tau}+P_3\frac{dP_3}{d\tau}$

時刻tを用いた位置（速度）および力を用いて表すと

$\frac{cdt}{d\tau}\frac{dP_0}{d\tau}=\sum _i\frac{dt}{d\tau}\frac{dx_i}{dt}\frac{dt}{d\tau}f_i=\left(\frac{dt}{d\tau}\right)^2\left(\vec{v}\cdot\vec{f}\right)$

式変形を行うと

$\left(\vec{v} \cdot \vec{f} \right )=\left(\frac{d\tau}{dt}\right)^2\frac{cdt}{d\tau}\frac{dt}{d\tau}\frac{dP_0}{dt}$

以上より次の結果が得られる。

$\frac{dP_0}{dt}=\frac{1}{c}\left(\vec{v} \cdot \vec{f} \right )$

式を評価すると右辺は仕事率を高速で割ったものである。

つまり

$P_0=\frac{E}{c}$

であることがわかる。

これまでの議論で導出された

$P_0=\frac{E}{c}$

$-\left(mc \right )^2=-P_0^2+P_1^2+P_2^2+P_3^2$

より

$-(mc)^2=-\left(\frac{E}{c}\right)^2+P_1^2+P_2^2+P_3^2$

$E=c\sqrt{(mc)^2+p^2}$

v<<cの時Taylor展開を行うと

$E=mc^2\sqrt{1+\left(\frac{mv}{mc}\right)^2 }\cong mc^2\left(1+\frac{1}{2}\left(\frac{mv}{mc} \right )^2 \right )=mc^2+\frac{1}{2}mv^2$

となり、静止質量エネルギーと運動エネルギーが導出できた。

第一回：　四次元時空の基礎知識

以下を定義する。

ローレンツ因子： $\gamma = \frac{1}{\sqrt{1-\left ( \frac{v}{c}^ \right )^{2}}}$

また、Cは光速を表す。

ミンコフスキー空間について

ミンコフスキー空間とは３次元空間に時間軸を加えた、４次元の空間である。

ベクトルAとベクトルBの内積を次のように定義する。

$\vec{A}\cdot \vec{B}= -A_{0}B_{0}+A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}$

これによりノルム（長さのようなもの）は

$A^{2}=-\left ( {A_{o}} \right )^2+\left ( A_{1} \right )^2+\left ( A_{2} \right )^2+\left ( A_{3} \right )^2$

また、ミンコフスキー空間において線素は

$\left(ds \right )^2=-\left(cdt \right )^2+\left(dx)^2+(dy)^2+(dz)^2$

と書ける。

固有時の定義

ここで固有時はτを用いて表す。

固有時とは物体と同じ速度の座標系で計測した時間のことで、数式で表すとｔを観測者の時間として

$\tau \equiv \int \frac{dt}{ \gamma }$

$\gamma d \tau =dt$

と表せる。

τの特徴としてはｔはLorentz変換に対して不変ではないのに対して、τは不変であることがあげられる。