以前の記事の続きです。
すごろくの問題は基本的に調べ上げで対応することになりますが、ゴールから考えるとうまくいくことが多いです。
たとえば次のような問題です。
すごろく①（慶應普通部2019）
下の図のＤに石を置きます。1から6の目があるサイコロをふって、奇数の目が出たら左へ、偶数の目が出たら右へ、出た目の数だけ石を動かします。たとえば、4が出たらＤ→Ｅ→Ｆ→Ｇ→Ｆへ、次に1が出たらＦ→Ｅへ石を動かします。
はじめにＤに石を置いた後、サイコロを3回ふって動かしたとき、石がＧにある目の出方は何通りですか。
ゴールから考える。
3回目に石がＧにあるということは3回目は右方向に動かすこととなる。「偶数の目が出たら右へ、出た目の数だけ」動かすルールだから、石は2回おわった時点でＥ、Ｃ、Ａのどこかにある必要。この3パターンに場合分けして考える。
❶2回おわってＥにあるとき、1回目の場所はＦ（そのあと1が出た）、Ｃ（そのあと2か6が出た）、Ａ（そのあと4が出た）の3つのどれか。
1回目でどう動くかもあわせて考えると、次のように合計7通りがある。
❷2回おわってＣにあるとき、❸2回おわってＡにあるときについても同じように考えると、次のように❷が5通り、❸が3通りある。
2回目→3回目はそれぞれ1通りに決まるので「石がＧにある目の出方」はぜんぶで15通り。
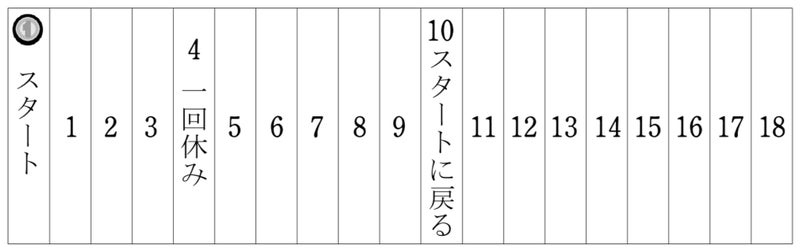
すごろく②（龍谷大学付属平安中2020前期C）
下の図において、サイコロを投げて、「スタート」の位置にあるコインを出た目の数だけ1マスずつ進めます。3回目でちょうど「13」の位置に止まる場合は何通りありますか。ただし、「1回休み」のところに止まった場合は、余分に1回サイコロを投げたことになります。また、「スタートに戻る」の位置に止まった場合は、スタートに戻ります。
これもゴールから考える。3回目にコインが「ちょうど「13」の位置に止まる」ような2回目の場所として7から12が候補となる。この6パターンに場合分けして考える。
❶2回おわって7にいるとき、（1回目，2回目）の組合せは（1，6）（2，5）（3，4）（4，3）（5，2）（6，1）の5通り（最初に4が出ると「1回休み」となり3回でゴールできなくなってしまう）
❷2回おわって8にいるとき、最初2回は（2，6）（3，5）（4，4）（5，3）（6，2）の4通り
❸2回おわって9にいるとき、最初2回は（3，6）（4，5）（5，4）（6，3）の3通り
❹2回おわって10にいることはない（10にとまるとスタートに戻るルールなので）
❺2回おわって11にいるとき、最初2回は（5，6）（6，5）の2通り
❻2回おわって12にいるとき、最初2回は（6，6）の1通り
2回目→3回目はそれぞれ1通りに決まるので、以上の❶～❻の合計で15通り 
