楕円曲線での演算は点と点同士の演算です.
普通の足し算・掛け算とは少し異なります.
次の図をご覧ください.
P1 * P2 から見ていきましょう.
P1 * P2 は 直線 P1P2 と 楕円曲線の交点です.
この演算を便宜上楕円乗算とします.
楕円曲線は x 軸に関して対称なので,
楕円乗算した点 P1 * P2 のy 座標の符号を反転させた点を
定義することができます.
この点を P1 + P2 と定義します.
この演算を楕円加算といいます.
P1 と P2 が重なった場合,つまり,
楕円曲線の接点となる場合は,
接線と交わる点を乗算の点とします.
こんな感じです.
楕円乗算は群を作りませんが,
楕円加算は群になります.
群をなすということは,
普通の足し算のゼロや
掛け算のイチに
相当するものはあるのでしょうか?
楕円加算では無限に遠い点Oを
普通の足し算のゼロと
同じように扱うことができます.
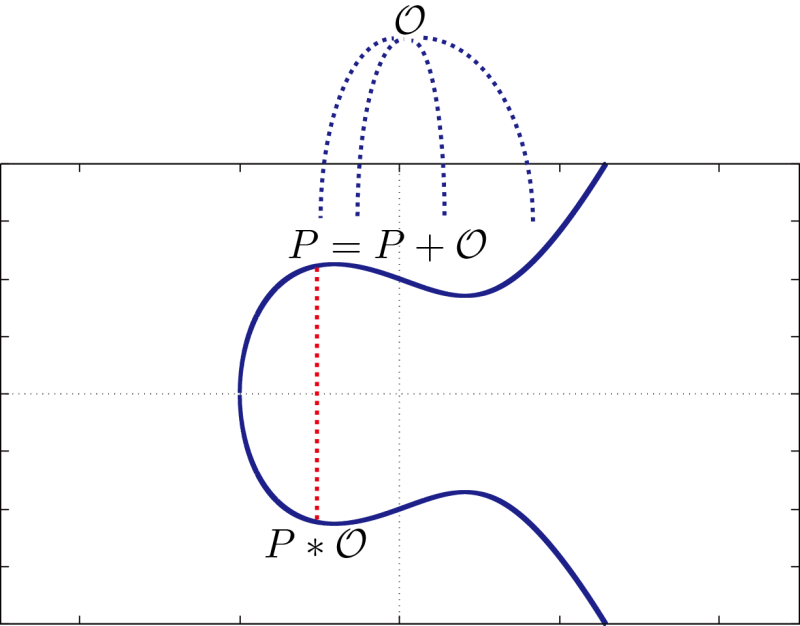
まず, x = (P の x 座標) のグラフ(中学校の教科書では削除されている)と
楕円曲線のもう一つの交点を P * O とします.
P * O の y 座標の符号を反転させると,あら不思議.
なんと,点 P に戻ってしまいます.
したがって, P * O は P の y 座標の符号を反転させたもの,
つまり, P の逆元と考えることができます.
また, P + O は P そのものだということができます.
これで単位元 O が存在することはわかりましたね.
結合法則は図を描いてみればわかります.
以上で,楕円加算は群をなすということがわかりました.
楕円乗算は群をなさないということもわかります.
これは,P * e = e * P = P となるような e が見つからないからです.
乗算して元にもどるようなものがありません.
図からわかります.
結合法則は満たすので,群よりももう少し範囲が大きい
半群の性質を満たします.

