半数の中学校で
1学期期末テストが終わりました。
早くも答案が返却されはじめた学校もある。
結果については、我々スタッフと講師とで
ひとりひとりの生徒についてミーティングを行い、
今回の反省と次回に向けての目標を設定し、
生徒本人とのやりとりも含め、
カリキュラムを再編成していく。
次は2学期中間テストです。
と、その前に
夏休みがやってくる。
受験生にとって
この夏は
本当に正念場。
受験の「天王山」とは
よく言われるセリフですが、
本当に、この夏の過ごし方で
受験の成否が大きく変化します。
スクールIEは、個性別指導の塾ですので、
「夏休みの勉強」と一言にいっても、
たとえば、
同じ学年で、同じ教科を受講している子たちが
同じ内容を学んでいるかというと、
そうでもありません。
その子の「現在位置」、「目標到達点」に応じて、
それぞれ別のことをしていきます。
しかし、
そうはいっても、
「これは外せない!」という分野もある。
たとえば、
中学3年生の数学においては
「関数」。
これが、この夏のテーマのひとつです。
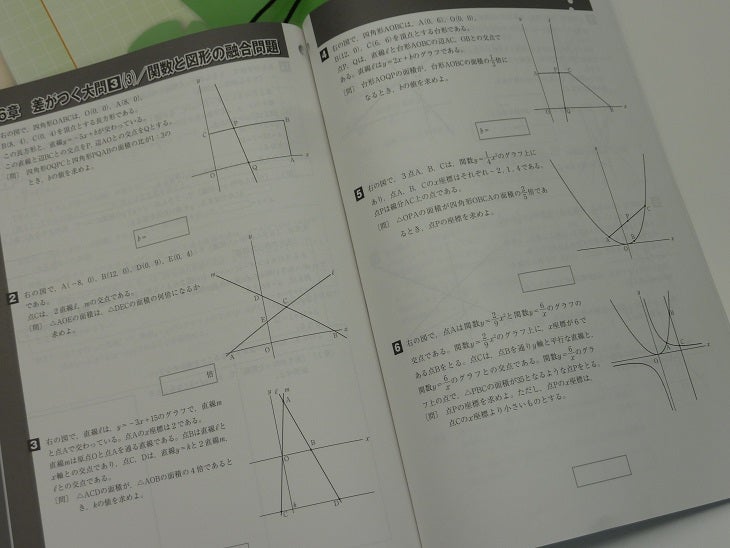
↑ こちら、都立高校入試対策を目した
関数の練習問題集。
いったい、関数については
都立高校入試の大問3を構成し、
そこそこの配点を有するのみでなく、
あらゆる私立校入試でも同じく大きな配点を有する。
さらに、
中学校2学期の数学においては、
二次関数が主要範囲となる。
関数をマスターすることは、
① 入試本番の学科試験対策
② 入試結果を大きく左右する内申点、
それを決定づける2学期定期テストの対策
という2つの理由において、
絶対的に重視しなければならないことである。
しかも、
苦手な生徒が多い。
中学3年生が
2学期に相対する関数は「2次関数」です。
しかし、その前提として、
1年生の「比例・反比例」、
2年生の「1次関数」があって、
これらがしっかり理解できていないと
2次関数のマスターは、難しい。
なので、
中学3年生の夏休み、
数学の授業内容のひとつとして、
「関数」の徹底学習をご提案しています。
全員にコレを使うわけではありませんが、
都立高校入試を目指す生徒たちに
ご提案する夏の勉強の教材のひとつが
これ ↓
文字通り、
都立高校入試対策問題集。
これを使って、
「関数」の対策も行ってまいります。
・・・「も」というのは、
もちろん、それ以外もやっていきたいので♪
↓
こちら、同じく都立入試
前半の練習問題。
序盤の問題をしっかりできるようにすることで、
得点のベースをつくります。
↑こちら、空間図形の対策。
↑関数の中でも、
少し難易度の高い問題集。
こうした内容・・・
たとえば「2次関数」という
大きな範囲をマスターするのに、
次回授業までのスパンが短い
講習会での学習は最適です。
もちろん、
都立志望の生徒と、
私立志望の生徒では、
「必要なこと」が異なっていきます。
「関数」の中でも、
難関私立校を目指す子の場合、
より応用度の高い問題への対応力をつけねばならない。
しかし、ともかく、
関数が「不要」という状況は
すべての生徒、あり得ない。
なので、
数学科では、
今回の夏で
2次関数までをマスターできるよう、
(・・・「まで」というのは、
つまり、1年生の比例・反比例、
2年生の1次関数も含めて、
必要なところからスタートするので)
指導に力を入れていきたいと思っています。
kama
↓ブログランキングに参加しています
応援クリック、よろしくお願いいたします^^