『１変数でしか使えぬ基礎たりえぬ応用利かぬ理論が、大学数学の基本として君臨』アチャ～な実体に注意

多変数のテーラー展開は、偏微分が出て来て、元になる点群に直交性必須　それを、判り良く紹介したかったのですが、意外に、

テーラー展開が難しく、（その限界を示す）簡単明解な説明は、今後の課題に…

時間）積分、行列式等の数学は完全思いますが、FEM等の離散計算の数学は問題。元来、独立変数で実施すべき偏微分を、

（直交線上にない）独立せぬ変数データ元に計算する変則（変数独立性満たさぬ、怪しい偏微分計算伴い、数学書は未記載）

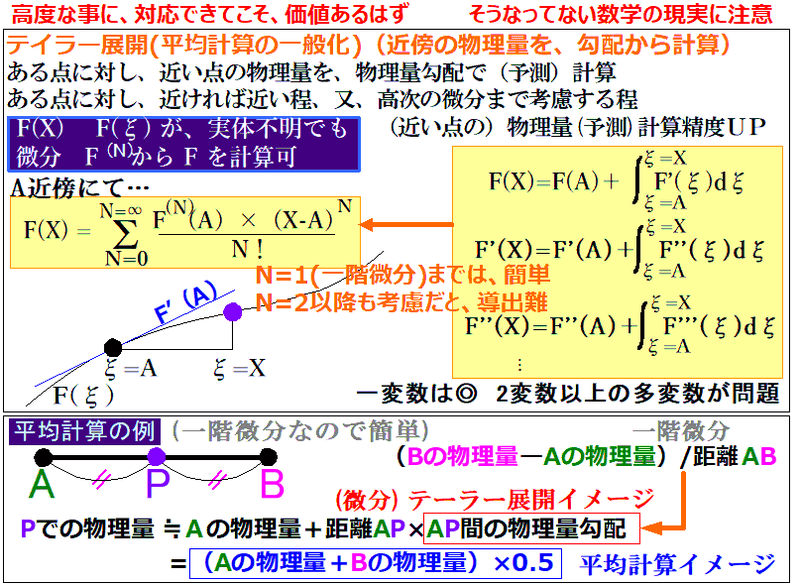
近似基礎テーラー展開は、高校数学レベルの簡単な一変数限定　正しい正統的数学では、直交格子までが限界に見えます

『１変数限定（テンソルは解けず）応用利かぬ理論が数学の基本として君臨』　多大な社会損失か、数学の限界で仕方なしか？

微分（dX等で記述される）は計算できるが、幾何の偏微分（∂X）は計算できず。それが数学の限界思います。

テイラ-展開を、２変数以上に拡張すると、偏微分（例えば∂X ∂Y）が出現してしまう。直交格子でのみ一変数dXやdYに同じとみなせる

偏微分＝直交直角向勾配(複数成分) を直交せぬ点群元に計算＝数学的に正しい計算策がない（点群に平行な方向、微分勾配計算までは可能）

点群向き方向、微分勾配計算までは計算可　（直角でない斜め向のテイラー展開のみ可。実際それを計算）実用十分いう事も多く、大変微妙ですが

直交メッシュ以外、偏微分の定義通りの計算不可で注意　（直交格子以外だと、偏微分Y成分を、X成分使って計算…　変数独立性に反する）

直交メッシュなら、（座標軸に沿うテイラー展開での微分で）偏微分を定義通り計算可。

テクニックに頼ると偏微分でなくなる（定義逸脱） そこが勉強の限界な感。打破できるか？ 打破すると偏微分でなくなるパラドクスがあるか？

テンソル計算（力学全域に影響及び致命的）　グラデーション計算行う３Dポリゴンデザイン分野　そこらは、幾何偏微分解く理論不完全で注意

後者3Ｄグラデーション画は ⇒ 粗悪モデルだと勾配または法線ベクトルが乱れ画質悪化 ⇒ メッシュ増加 又は調整 で解消

前者テンソルは、２階偏微分必須。３Dグラデーション計算よりもシビア＆神経質で注意。　テンソルは、工学全域に関わり重大

（直交物理量の差の差の計算）二階偏微分必須で超難「テンソルは、(完全には)解けません」程度は、教科書に記述して欲しい。でないと…　

テイラー展開は、有用性-応用性ｰ拡張性ｰ融通性高いが故、数学における基本として重視されている（筈）　そう勘違ってしまう。

離散化では、幾何偏微分を、直角向でない、点の並び方向から計算せざるを得ず、テイラー展開で（直交勾配たる）偏微分は解けず

その解釈が妥当な筈。（アイソパラメトリック要素では、点並び向にテイラー展開を使うが、直交勾配に変換する変則技も利用）

「直交勾配への変換技まで、数学的に正しい」　思っている人が多いかも…　直角向でない斜め方向からの（回転写像含まぬ）変則変換技ですが…

テイラー展開=１変数限定理論。敢えて、2変数以上なら、（軸に平行な勾配成分）例えば ∂X ∂Y 計算必須。点群が軸に平行＆直交分布でないと厳密計算困難

それが出来てない）怪しい手法ながら、離散計算アプリは普及＆実用済。実は、理論云々は、後回し。製品化＆マーケット支配が先 ？

理論完全化を待っていては、又は、数学上厳密な範囲内に終始していては、実用到達せず＆成果得られず＆出遅れ間に合わず？　具体的には…

ξ-η⇔X-Y 離散計算に必須。上式はテーラ展開応用ともいえるが、ξ-η直交直角が上記等式必須成立条件。だと直交メッシュ限定

ξ-η直交せぬ変則系で自在形状に適応させる手法が離散計算理論。実はξ-η直角以外は正確な等式成立でない＆正しい数学でない

テイラー展開超える、使える理論打立てねばならない。が出来てない。微分は解ける＆偏微分は解けず。だと工学では欠陥

基礎として欠陥なテイラー展開が君臨せざる得ず＆対処策見出せずズルズル…　そこが数学の（超痛い）致命的限界！？

『大変痛いッ！』　判り良く書籍に書いて欲しい感。限界ある理論を根幹に据えねばならぬ。それしか策なしか？　仕方なしか？