ピタゴラスの定理【内上】ピタゴラス数/の性質・・
ピタゴラスの定理の証明
この定理には数百通りもの異なる証明が知られている。ここにいくつかの代表的な証明を挙げる。
以下では頂点 A, B, C からなる三角形を △ABC と表す。また、各辺 AB, BC, CA に向かい合う角をそれぞれ ∠C, ∠A, ∠B と表し、各頂点 A, B, C の対辺BC, CA, AB の長さをそれぞれ a, b, c と表す。 頂点の記号は直角三角形 △ABC の直角が ∠C になるように与える。
相似による証明
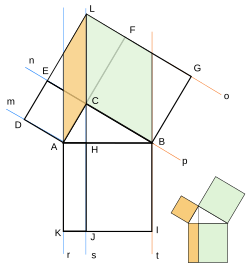
相似を用いた証明
頂点 C から斜辺 AB に下ろした垂線の足を H とする。△ABC, △ACH, △CBH は互いに相似である。よって △ABC と △ACH の相似比より
- {\displaystyle {\text{AC}}:{\text{AH}}={\text{AB}}:{\text{AC}}\Longrightarrow {\text{AH}}={{\text{AC}}\times {\text{AC}} \over {\text{AB}}}={b^{2} \over c}}
であり、同様に △ABC と △CBH の相似比より
- {\displaystyle {\text{BH}}={a^{2} \over c}}
である。したがって
- {\displaystyle c={\text{AB}}={\text{AH}}+{\text{BH}}={b^{2} \over c}+{a^{2} \over c}}
であるから、両辺に{\displaystyle c} を掛けて
- {\displaystyle c^{2}=a^{2}+b^{2}}
を得る。
正方形を用いた証明
正方形を用いた証明
△ABC と合同な4個の三角形を図のように並べると、外側に一辺が a + b の正方形(以下「大正方形」)が、内側に一辺が c の正方形(以下「小正方形」)ができる。
- (大正方形の面積)=(小正方形の面積)+(直角三角形の面積)× 4
である。大正方形の面積は (a + b)2, 小正方形の面積は c2, 直角三角形4個の面積の合計は
- {\displaystyle {ab \over 2}\times 4=2ab}
である。これらを代入すると、
- {\displaystyle (a+b)^{2}=c^{2}+2ab}
整理して
- {\displaystyle a^{2}+b^{2}=c^{2}}
を得る。
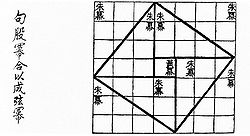
幾何学的な証明
『周髀算経』におけるピタゴラスの定理の証明(中国語: 句股冪合以成弦冪)
内接円を用いた証明
△ABC の面積 S は
{\displaystyle S={\frac {ab}{2}}}
(1)
{\displaystyle c=(a-r)+(b-r)}
(2)
であり、(2) を半径 r について解くと
{\displaystyle r={\frac {a+b-c}{2}}}
(3)
となる。三角形の面積 S を内接円の半径 r を用いて表すと
{\displaystyle S={r(a+b+c) \over 2}}
(4)
{\displaystyle {ab \over 2}={(a+b-c)(a+b+c) \over 4}}
(5)
(5) を整理すると
{\displaystyle a^{2}+b^{2}=c^{2}}
(6)
が得られる。
オイラーの公式を用いた証明
三角関数と指数関数は冪級数によって定義されているものとする。(指数法則やオイラーの公式の証明に本定理が使用されない定義であればよい。)まず sin2 θ + cos2 θ = 1 が任意の複素数 θ に対して成り立つことを(3通りの方法で)示す。
オイラーの公式より
- {\displaystyle {\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}}
または
- {\displaystyle {\begin{aligned}\sin ^{2}\theta +\cos ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}+\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}+{\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {4}{4}}=1\end{aligned}}}
もしくは、オイラーの公式から三角関数の半角の公式を導出する。
- {\displaystyle {\begin{aligned}\sin ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}\\&={\frac {1-\cos 2\theta }{2}}\ ,\\\cos ^{2}\theta &=\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {1+\cos 2\theta }{2}}\ .\end{aligned}}}
-
{\displaystyle \therefore \sin ^{2}\theta +\cos ^{2}\theta =1.}
(1)
(1) の式はピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている。
(1) の時点ですでに単位円上において本定理の成立が明らかである。なぜならば、本定理の逆は本定理を用いずに証明可能であるし、単位円上の任意の点の座標は (cosθ, sinθ) で表せるからである。
さて、前提とした △ABC について考え、∠A = θ とおけば
- {\displaystyle a=c\cdot \sin \theta }
- {\displaystyle b=c\cdot \cos \theta }
したがって
{\displaystyle a^{2}=c^{2}\sin ^{2}\theta }
(2)
{\displaystyle b^{2}=c^{2}\cos ^{2}\theta }
(3)
{\displaystyle a^{2}+b^{2}=c^{2}(\sin ^{2}\theta +\cos ^{2}\theta )}
(4)
- {\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。
三角関数の微分公式を用いた証明
正弦および余弦関数を微分すれば
{\displaystyle (\sin \theta )'=\cos \theta }
(1)
{\displaystyle (\cos \theta )'=-\sin \theta }
(2)
- {\displaystyle (\sin ^{2}\theta +\cos ^{2}\theta )'=2\sin \theta \cos \theta +2\cos \theta (-\sin \theta )=0}
したがって
- {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =C}
ここで C は定数である。θ = 0 を代入すると sin 0 = 0, cos 0 = 1 であるので、C = 1 が得られる。よって
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
(3)
が得られる。 ここで、前提とした △ABC について考え、∠A = θ とおいて、(3) および、三角関数と直角三角形の関係を考慮すれば
- {\displaystyle a^{2}+b^{2}={a^{2}+b^{2} \over 1}={a^{2}+b^{2} \over \sin ^{2}\theta +\cos ^{2}\theta }={a^{2}+b^{2} \over {a^{2}+b^{2} \over c^{2}}}=c^{2}}
が得られる。
三角関数の不定積分を用いた証明
下記のように関数を定める。
- {\displaystyle {\begin{aligned}f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta .\end{aligned}}}
上記を漸化式を利用して不定積分すると
- {\displaystyle {\begin{aligned}\int f(\theta )d\theta &=\int (\sin ^{2}\theta )d\theta +\int (\cos ^{2}\theta )d\theta \\&=\left({1 \over 2}\theta -{1 \over 2}\sin \theta \cos \theta +C_{1}\right)+\left({1 \over 2}\theta +{1 \over 2}\sin \theta \cos \theta +C_{2}\right)\\&=\theta +C_{1}+C_{2}\end{aligned}}}
である。微分積分学の基本定理を考慮し、これを微分すると
- {\displaystyle {\begin{aligned}{\frac {d}{d\theta }}\left\{\int f(\theta )d\theta \right\}&=f(\theta )&={\frac {d}{d\theta }}(\theta +C_{1}+C_{2})&=1\end{aligned}}}
である。したがって
- {\displaystyle {\begin{aligned}f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta &=1.\end{aligned}}}
ゆえに、ピタゴラスの定理は成立する。
三角関数の加法定理を用いた証明
三角関数は級数など(幾何以外の原理)によって定義されているものとし、オイラーの公式など(証明に本定理を使用しない方法)によって導出された三角関数の加法定理を用いれば
- {\displaystyle 1=\cos 0=\cos(\theta -\theta )=\cos \theta \cos \theta +\sin \theta \sin \theta =\cos ^{2}\theta +\sin ^{2}\theta }
または
- {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =\sin \theta \cos \left({\frac {\pi }{2}}-\theta \right)+\cos \theta \sin \left({\frac {\pi }{2}}-\theta \right)=\sin {\frac {\pi }{2}}=1}
が得られる。 また、加法定理を応用した三角関数の積和公式を用いて
- {\displaystyle {\begin{aligned}\sin ^{2}\theta &={\frac {\cos(\theta -\theta )-\cos(\theta +\theta )}{2}}\\&={\frac {1-\cos 2\theta }{2}}\end{aligned}}}
- {\displaystyle {\begin{aligned}\cos ^{2}\theta &={\frac {\cos(\theta -\theta )+\cos(\theta +\theta )}{2}}\\&={\frac {1+\cos 2\theta }{2}}\end{aligned}}}
したがって
- {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
が得られる。 両辺に c 2 を乗算して
- {\displaystyle c^{2}\sin ^{2}\theta +c^{2}\cos ^{2}\theta =c^{2}}
ここで、前提とした △ABC について考え、∠A = θ とおいて、三角関数と直角三角形の関係を考慮すれば
- {\displaystyle c^{2}\times \left({a \over c}\right)^{2}+c^{2}\times \left({b \over c}\right)^{2}=c^{2}}
よって
- {\displaystyle a^{2}+b^{2}=c^{2}}
が得られる。




 を掛けて
を掛けて