あなたは、式を立てるとき、どうしていますか?
問題を読んですぐに立式できますか?
自信がある人も、今日の問題を見たら、
「えー、ちょっと…」
と、戸惑うと思います。
そんなあなたに向けて書きました。
挑戦してください。
感想を教えてもらえると、更に、うれしくなります。
では、6年生の算数の問題です。
早速、挑戦してください。
(問題)
青いペンキは、3dLで8/5㎠の板をぬれます。
では、青いペンキ1dLでは、何㎠の板がぬれるでしょう?
A:「青いペンキ1dLでは、何㎠の板がぬれるでしょう?
これが、たずねていることだね」
T:「A君、すぐに気づいたね。さすがだね」
B:「『青いペンキは、3dLのとき、8/5㎠の板がぬれる』と書いてあるね。
8/5㎠、分数になると、よくわかんないよ」
C:「3dLのとき、9㎠の板がぬれるなら、すぐにわかるのに」
A:「それなら、1dLのとき、
式は、9÷3=3。答えは、3㎠になるね」
C:「つまり、1dLのとき、3㎠ぬれるってことか」
A:「すぐに出るね」
C:「分数を整数に置き換えてる」
B:「これって、すごいことだよ。だって、『小数や分数のときは、整数に置き換えてみる』といいって、先生が言っていたことを思い出したよ」
T:「Bさん、よく覚えていたね」
C:「Bさん、すごーい」
A:「式は、8/5 ÷ 3でできるんじゃない」
B:「さすがA君」
A:「でも、自信がないよ」
T:「では、数直線図で考えてみようか」
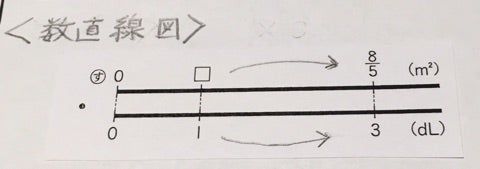
数直線図(1)
T:「3dLのとき、8/5㎠だから、数直線図に書けるね」
A:「はい、書けます」
T:「求めるのは、1dLのときに□㎠だね」
B:「そうか、下が1でその上が□となるね」
C:「あー、そうか、数直線図だと、よくわかるね」
T:「下のdLでみると、どうなっている?」
B:「1から3、つまり、3倍になっています」
T:「そうだね。では、上の方は、どうなると思う?」
C:「同じように、3倍になると思います」
B:「私も同じです」
A:「ぼくもそう思います」
T:「3人とも分かってきたようだね」
T:「3dLのとき、8/5㎠だから、数直線図に書けるね」
A:「はい、書けます」
T:「求めるのは、1dLのときに□㎠だね」
B:「そうか、下が1でその上が□となるね」
C:「あー、そうか、数直線図だと、よくわかるね」
T:「下のdLでみると、どうなっている?」
B:「1から3、つまり、3倍になっています」
T:「そうだね。では、上の方は、どうなると思う?」
C:「同じように、3倍になると思います」
B:「私も同じです」
A:「ぼくもそう思います」
T:「3人とも分かってきたようだね」
数直線図(2)
T:「では、どんな式になると思いますか?」
B:「 □ × 3 = 8/5 」
C:「ぼくも同じです」
T:「A君、この式を解いてくれる?」
A:「はい、
□ × 3 = 8/5
□ = 8/5 ÷ 3
=8/5 × 1/3
=8/15
答えは、8/15 です」
C:「つまり、1dLで、8/15㎠ ぬれるということになります」
T:「C君、まとめてくれてありがとう」
A:「今回、数直線でやって見て、よーく分かりました」
B:「私は、整数に置き換えるは、分かっていたけれど、数直線図でやって、つながりました」
C:「数直線図の良さが、実感できました。
ありがとうございます」
これで、今日の算数タイムは終わりです。
T:「では、どんな式になると思いますか?」
B:「 □ × 3 = 8/5 」
C:「ぼくも同じです」
T:「A君、この式を解いてくれる?」
A:「はい、
□ × 3 = 8/5
□ = 8/5 ÷ 3
=8/5 × 1/3
=8/15
答えは、8/15 です」
C:「つまり、1dLで、8/15㎠ ぬれるということになります」
T:「C君、まとめてくれてありがとう」
A:「今回、数直線でやって見て、よーく分かりました」
B:「私は、整数に置き換えるは、分かっていたけれど、数直線図でやって、つながりました」
C:「数直線図の良さが、実感できました。
ありがとうございます」
これで、今日の算数タイムは終わりです。