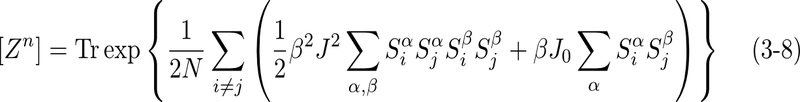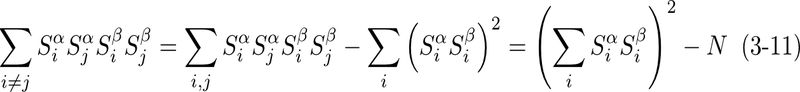図1.イジングモデル
前回まではイジングモデルの性質を導いてきたが、今回はスピン間相互作用Jが定数ではなく、i番目のスピンと、隣り合うスピンjに依存した変数Jijに置き換え、外部磁場の影響を無視したモデルを考える。このようなモデルはEA(エドワーズ・アンダーソン)モデルと呼ばれ、この系のエネルギーは
で与えられる。ここで、ijが取りうる全ての組合わせの平均を[・・・]で表わし、配位平均と呼ぶとする。また、系全体のスピン間相互作用Jijの分布について、ガウス分布を仮定する。Jijの平均を[Jij]=J0、分散を[(⊿Jij)2]=J2とすると、ガウス分布の確率密度関数は
と書ける。これらの前提を踏まえた上で、前々回の式(1-6)
と同じく式(1-8)
を用いると、自由エネルギーの配位平均は
で得られる。ここで、ボルツマン定数kB=1としたため、1/β=Tである。この式(3-3)を具体的に求めることは困難であるため、主要な近似法としてレプリカ法を用いる。具体的には、
と置き換えて計算を進める。これは、n個の系のレプリカを仮定して、その全ての分配関数の配位平均[Zn]を求め、n→0の極限を取ることで、近似によって[lnZ]の計算を避けることができる。しかし、レプリカ法を用いても、EAモデルの[F]は求めることは難しいため、平均場理論に頼ることにする。
前回の無限レンジモデルの厳密解より、無限レンジモデルが平均場近似と同等の結果を与えることを利用する。すなわち、EAモデルの無限レンジの場合を考えると、系のエネルギーは
となる。ここで、前回同様にエネルギーの次元O(N)に揃える必要があるため、Jijの平均を[Jij]=J0/N、分散を[(⊿Jij)2]=J2/Nとして、Jijについてのガウス分布を書き換えると
となる。このモデルはSK(シェリントン・カークパトリック)モデルと呼ばれる。これより、SKモデルにレプリカ法を用いるために、[Zn]について求める。分配関数の定義(1-6)より、系のエネルギー(3-5)と、Jijの分布(3-6)を用いると
となる。ここで、αはレプリカの番号を示す。また、分配関数は場合の数であるため、i,jについての組合せは総乗になる。さらに、系が取り得る自由度についての総和は、表記が煩雑になることを避けるために、行列のTrで表わした。これより、i,jについて独立に積分を実行できるため、ガウス分布の積率母関数を用いると
となる。この式のαについてのnが十分大きい場合、αについてのΣとスピンは
と書き直せるため、これを用いると、式(3-8)は
と書き直せる。ここで、Trの前の係数は、全体から見て影響が小さいため、これ以降の議論では省略する。i,jについてのNが十分大きい場合、i,jについてのΣとスピンは逆に書き換えて
となる。これを用いると、式(3-10)は
となる。ここで、括り出せる係数は省略した。この式(3-12)の(ΣiSiαSiβ)2について、積分定数をqαβとして、前回の公式(2-4)
を用いて
として適用すると
となる。ここで、係数は省略した。同様に、(ΣiSiα)2について、積分定数をmαとして、公式(2-4)を
として適用すると
となる。これより、式(3-14)と式(3-16)を用いて、式(3-12)を書き直すと
となる。式(3-17)の2行目の部分は、特定の1つのiについて、Trを展開すると
と書ける。ここで、Lを
と置いた。この式(3-18)を用いると、式(3-17)は
となる。
出典:HIDETOSHI NISHIMORI. Statistical Physics of Spin Glasses and Information Processing An Introduction
P11 2.MEAN-FIELD THEORY OF SPIN GLASSES
―――――――――――――――――――――――――――――――――――――――――――
[Zn]を求めただけだが、文字数制限の関係から今回はここまで。細かい部分で特殊な計算をしているが、大枠は前回の無限レンジモデルの厳密解に則っている。
議論の上で重要な部分としては、スピン間相互作用をより一般的に拡張したこと、それに伴い計算上の解決策としてレプリカ法を用いたことである。特にレプリカ法の近似式は、分配関数の数を連続的に取り扱っていることから、数学的な妥当性が立証されていない。しかし、それが原因となる問題は発見されていないようなので、本項でもこの手法を用いることにする。
最終的に、この[Zn]を用いて得られる状態方程式は、次の項SKモデルのレプリカ対称解で求めていきたい。
 |
Statistical Physics of Spin Glasses and Informa...
13,167円
Amazon |