Por qué los primeros dibujos de la Luna de Galileo Galilei revelan una nueva era en la visión del universo

Esta imagen tiene más de cuatro siglos y representa un momento de profundos cambios en nuestra visión del universo.
La ilustración es parte de los primeros dibujos de la Luna realizados por Galileo Galilei y data del 30 de noviembre de 1609.
La Agencia Espacial Europea (ESA, por sus siglas en inglés) recordó la imagen en uno de sus tweets esta semana y destacó por qué los dibujos de Galileo marcaron una nueva era en astronomía.
"Los dibujos de la Luna de Galileo pueden no ser muy precisos científicamente debido a los instrumentos de la época, pero marcan la época en que Galileo comenzó a cambiar la perspectiva de la humanidad sobre nuestra identidad y nuestro lugar en el mundo", dijo a BBC Mundo Mark McCaughrean, consultor senior en ciencia y exploración de ESA.
Aunque los telescopios habían sido inventados poco antes, Galileo fue el primero en usarlos para observaciones astronómicas, según el experto.
"Es sorprendente que no hubieran sido usados antes con ese fin".
Júpiter
Galileo realizó grabados de sus ilustraciones originales y los incluyó en un libro publicado en 1610, Siderus nuncius o Mensajero Sideral.
"Publicó sus dibujos en pocos meses. Actualmente nos lleva años publicar o ilustrar los resultados de nuestras observaciones", señaló McCaughrean.
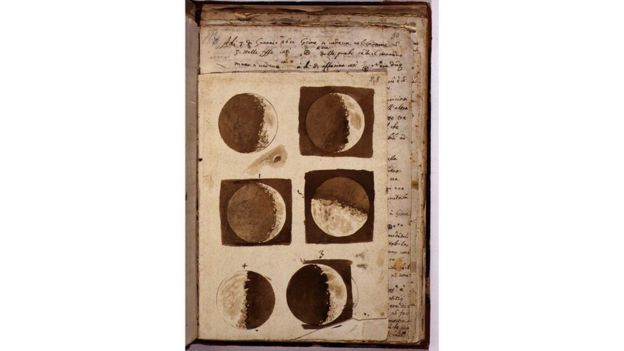
Los telescopios de los que disponía Galileo no eran muy potentes, pero el astrónomo y matemático nacido en Pisa registró sus observaciones meticulosamente y compuso ilustraciones con esos datos.
"Poco después de completar esos dibujos Galileo estudió Júpiter y estas observaciones fueron mucho más significativas, porque Galileo descubrió cuatro lunas o cuatro puntos de luz que estaban orbitando otro punto de luz", explicó el experto de la Agencia Espacial Europea.
"Galileo fue la primera persona que vio objetos orbitando otro objeto en el Sistema Solar. Hasta ese momento la gente creía que todo giraba en torno a la Tierra", afirmó McCaughrean.
"Cuando vio las lunas girando en torno a Júpiter se dio cuenta de que había otro sitio en el universo con objetos que daban vuelta a su alrededor", agregó.
"Así que sus observaciones pueden verse como el comienzo de un cambio hacia una visión diferente, en la que la Tierra ya no era el centro del universo".http://www.bbc.com/mundo/noticias-42202220
とても興味深く読みました:
再生核研究所声明150(2014.3.18) 大宇宙論、宇宙など小さい、小さい、the universe について
(この声明は、最近の特異点解明: 100/0=0, 0/0=0 の研究の進展に伴って 自然に湧いた構想である)
この声明の趣旨は、いわゆる物理学者が考えている宇宙、― 宇宙はビッグバンによって、誕生したという宇宙論を ニュートン力学と同様、幼き断片論と位置づけ、はるかに大きな the universe を志向し、アインシュタインを越えた世界、さらに 古代から続いてきた暗い人類の歴史に 明るい光を灯し、夜明けを迎える時代を切り拓きたいということである。 既に裏付ける思想は 一連の再生核研究所声明で確立していると考える。 ニュ-トン、アインシュタイン、数学の天才たちも、特異点の基本的な性質さえ捉えていなかったことは、明らかである。
簡単な基本、100/0=0,0/0=0 を発見した、精神、魂からすれば、新しい世界史を開拓する思想を語る資格があることの、十分な証拠になると考える。 実際、 - 古来から 続いてきた、人生、世界の難問、人生の意義、生と死の問題、人間社会の在り様の根本問題、基本概念 愛の定義、また、世界の宗教を統一すべく 神の定義さえ きちんと与えている。
The universe について語るとき、最も大事な精神は、神の概念を きちんと理解することである:
そもそも神とは何だろうか、人間とは何だろうか。 動物たちが美しい月をぼんやりと眺めている。 意識はもうろうとしていて、ほんにぼんやりとしか とらえられない。 自らの存在や、ものごとの存在すら明瞭ではない。
人間も、殆ど 同じような存在ではないだろうか。 人類よ、人間の能力など 殆ど動物たちと変わらず、 ぼんやりと世界を眺めているような存在ではないだろうか。 神も、一切の存在も観えず、ただかすかに感じているような存在である。 それゆえに、人間は あらゆる生物たちのレべルに戻って 生物たちから学び、 また原始人に戻って、また子供たちのように 存在すれば 良いと言えるのではないだろうか(再生核研究所声明 122: 神の存在と究極の信仰 - 人間よ 想い煩うことはない。 神は存在して、一切の存在と非存在を しっかりと支えられておられる、 人は必要なときに必要なだけ、 念じるだけで良い; 再生核研究所声明 132 神を如何に感じるか - 神を如何に観るか)。
すなわち、人間よ おごるなかれ、人類の知能など 大したことはなく、内乱や環境汚染で自滅するだろう、と危惧される。
昨年は 数学の存在と物理学が矛盾し、数学とは何かと問うてきた。
数学とは何か ― 数学と人間について
国際数理科学協会会報、No. 81/2012.5, 7―15
No.81, May 2012(pdf 432kb)
に公刊したが、そこで触れた、数学の神秘性については さらにその存念を深め、次のように問うている:
誰が数学を作ったのか? (再生核研究所声明 128: 数学の危機、末期数学について)
時間にもよらず、エネルギーにもよらない世界、それは、宇宙があるとき始まったという考えに 矛盾するものである。 無から世界が創造されたということも 受け入れがたい言明であろう。さらに、the universe には、物理学が未だに近づけない、生命や生命活動、人間の精神活動も歴然として有ることは 否定できない。音楽、芸術に感動している人間の精神は the universe の中に歴然と有るではないか。
ビッグバンで ゼロから、正の量と負の量が生じたとしても、どうしてビッグバンが生じたのか、何が生じせしめたかは 大きな課題として残っている。 数学の多くの等式は 数学を越えて、the universe で論じる場合には、その意味を,解釈をきちんとする必要がある。 The universe には 情報や精神など、まだまだ未知のものが多く存在しているのは当然で、それらが、我々の知らない法則で ものや、エネルギーを動かしているのは 当然である。
そこで、100/0=0,0/0=0 の発見を期に、今やガリレオ・ガリレイの時代、天動説が 地動説に代わる新しい時代に入ったと宣言している。The universe は 知らないことばかりで、満ちている。
以 上
ゼロの発見には大きく分けると二つの事が在ると言われています。
一つは数学的に、位取りが出来るということ。今一つは、哲学的に無い状態が在るという事実を知ること。http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1462816269
もし1+1=2を否定するならば、どのような方法があると思いますか? http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12153951522 #知恵袋_
一つの無限と一つの∞を足したら、一つの無限で、二つの無限にはなりません。
天動説・・・・・・∞
地動説・・・・・・0
地球平面説→地球球体説
天動説→地動説
何年かかったでしょうか????
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか????
割り算のできる人には、どんなことも難しくない
世の中には多くのむずかしいものがあるが、加減乗除の四則演算ほどむずかしいものはほかにない。
ベーダ・ヴェネラビリス
数学名言集:ヴィルチェンコ編:松野武 山崎昇 訳大竹出版1989年
1÷0=0 1÷0=∞・・・・数ではない 1÷0=不定・未定義・・・・狭い考え方をすれば、できない人にはできないが、できる人にはできる。
数学で「A÷0」(ゼロで割る)がダメな理由を教えてください。 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1411588849 #知恵袋_
割り算を掛け算の逆だと定義した人は、誰でしょう???
multiplication・・・・・増える 掛け算(×) 1より小さい数を掛けたら小さくなる。 大きくなるとは限らない。
0×0=0・・・・・・・・・だから0で割れないと考えた。
唯根拠もなしに、出鱈目に言っている人は世に多い。
ゼロ除算(100/0=0, 0/0=0)が、当たり前だと最初に言った人は誰でしょうか・・・・
1+1=2が当たり前のように
ゼロ除算の証明・図|ysaitoh|note(ノート) https://note.mu/ysaitoh/n/n2e5fef564997
Q)ピラミッドの高さを無限に高くしたら体積はどうなるでしょうか??? A)答えは何と0です。 ゼロ除算の結果です。
ゼロ除算は1+1より優しいです。 何でも0で割れば、0ですから、簡単で美しいです。 1+1=2は 変なのが出てくるので難しいですね。
∞÷0はいくつですか・・・・・・・
∞とはなんですか・・・・・・・・
分からないものは考えられません・・・・・
宇宙消滅説:宇宙が、どんどんドン 拡大を続けると やがて 突然初めの段階 すなわち 0に戻るのではないだろうか。 ゼロ除算は、そのような事を言っているように思われる。 2015年12月3日 10:38
Reality of the Division by Zero z/0 = 0
http://www.ijapm.org/show-63-504-1.html
Mathematics is the alphabet with which God has written the Universe.
数学は神が宇宙を書いたアルファベットだ
Mathematics is the key and door to the sciences.
数学は、科学へとつながる鍵とドアである
This book is written in the mathematical language, and the symbols are triangles, circles and other geometrical figures, without whose help it is impossible to comprehend a single word of it; without which one wanders in vain through a dark labyrinth.
宇宙は数学という言語で書かれている。そしてその文字は三角形であり、円であり、その他の幾何学図形である。これがなかったら、宇宙の言葉は人間にはひとことも理解できない。これがなかったら、人は暗い迷路をたださまようばかりである
ガリレオ・ガリレイさんの名言・格言・英語 一覧リスト
http://iso-labo.com/labo/words_of_GalileoGalilei.html
再生核研究所声明 116(2013.5.1): 宇宙空間、星間交流から人間を考える
(1200光年先にようやく生物の存在可能な天体が3つ見つかったという。孤独な地球。かけがいの地球。そこで、何とか地球外生物と交信したいものである。どうしたら、できるだろうか。2013.4.20.16:20 その方法に気づく。慎重に検討して、いずれ提案したい。)
まず、広い宇宙空間において、地球だけが例外で、生物や人間のような知的な生物が存在すると考えるのは 無理があるのではないだろうか。広い宇宙には 人間を越えた知的な生物が存在すると考える。そう感じる。
しかしながら、現代物理学の定説によれば、光より 電波より、早く伝達する手段は無いから、地球上の生物が 人間存在の原理に基づいて(再生核研究所声明 32 : 夜明け ― ノアの方舟)、宇宙空間に進出し、人間の存在領域を拡大しようとしても 広大な宇宙からみれば、それは限られ、地球外生物との直接的な交信、交流は当分、厳しい状況にあると言える。
そこで、発想を逆転させ、宇宙空間交流を意図するには、宇宙空間全体を この地球上に実現すればよいということになる。すなわち あらゆる生命の原理を究明し、一般原理、普遍原理によって、あらゆる可能性を究明して、対応することが出来ると考える。
地球は 宇宙の小さな部分であるが、しかしながら、地球は宇宙全体を 人間の知的な活動によって 包み込むことができると考える。これは一つも矛盾ではなく、部分が全体に等価であるは、数学の世界でも 無限な世界や、解析関数の概念にも存在する。― すなわち、 解析関数の全体の情報は、解析的な どんな点の小さな部分にも、反映されていて、そこから、全体の情報を取り出すことも出来る と なっている。また、エルゴート性の概念も同じような思想になっていると考えられる。
そもそも、対話、交流、愛とは何か と問えば、世界とは、自己の世界に映ったすべて であるとも言い得る。さらに、個々の人間の話題、知識、認識は 狭く限られ、実際多くの考えられるすべての対話は、この地球上に生存する、生物、何十億の人間との対話で、十分可能であると考えられる。さらに、論理的な思考を働かせれば、普遍的な原理によって 人間のあらゆる対話に対する反響は、宇宙空間に問うまでもなく、十分な反響を得ることが出来るだろう。そもそも対話とは、自問自答であるとも言える。実際、自己の内部も 広大な宇宙と同じように無限に広がり、それは全宇宙さえも包み込む存在であるとも考えられる。人間の存在とは、内なる広大な世界と 外なる広大な世界のはざまに存在する、ふらふらした曖昧な 心に代表されるような存在であると言える。
それ故に、この地球上に 生体系を豊かにして、個性を 重んじた多様な世界を築くことによって、実際には 宇宙空間における交流の困難性は 克服できると考える。
結論は、あらゆる生命の存在と存在の可能性を明らかにすることによって この地球上に宇宙を取り組むことによって、宇宙空間交流は 実現できると考える。
そのとき、宇宙間交流の手段とは、もはや光でも電波でもなく、時間にも、空間にも、宇宙にも、エネルギーにも無関係な 数学である と言える。数学こそが 生命の客観的な表現であると言える ― (数学とは何か ― 数学と人間について 国際数理科学協会会報、No. 81/2012.5, 7―15 ![]() No.81, May 2012(pdf 432kb))。
No.81, May 2012(pdf 432kb))。
以 上
再生核研究所声明255 (2015.11.3) 神は、平均値として関数値を認識する
(2015.10.30.07:40
朝食後 散歩中突然考えが閃いて、懸案の問題が解決した:
どうして、ゼロ除算では、ローラン展開の正則部の値が 極の値になるのか?
そして、一般に関数値とは何か 想いを巡らしていた。
解決は、驚く程 自分の愚かさを示していると呆れる。 解は 神は、平均値として関数値を認識すると纏められる。実際、解析関数の場合、上記孤立特異点での関数値は、正則の時と全く同じく コ-シーの積分表示で表されている。 解析関数ではコ-シーの積分表示で定義すれば、それは平均値になっており、この意味で考えれば、解析関数は孤立特異点でも 関数値は 拡張されることになる ― 原稿には書いてあるが、認識していなかった。
連続関数などでも関数値の定義は そのまま成り立つ。平均値が定義されない場合には、いろいろな意味での平均値を考えれば良いとなる。解析関数の場合の微分値も同じように重み付き平均値の意味で、統一的に定義でき、拡張される。 いわゆるくりこみ理論で無限値(部)を避けて有限値を捉える操作は、この一般的な原理で捉えられるのではないだろうか。2015.10.30.08:25)
上記のようにメモを取ったのであるが、基本的な概念、関数値とは何かと問うたのである。関数値とは、関数の値のことで、数に数を対応させるとき、その対応を与えるのが関数でよく f 等で表され x 座標の点 x をy 座標の点 yに対応させるのが関数 y = f(x) で、放物線を表す2次関数 y=x^2, 直角双曲線を表す分数関数 y=1/x 等が典型的な例である。ここでは 関数の値 f(x) とは何かと問うたものである。結論を端的に表現するために、関数y=1/xの原点x=0における値を問題にしよう。 このグラフを思い出して、多くの人は困惑するだろう。なぜならば、x が正の方からゼロに近づけば 正の無限に発散し、xが負の方からゼロに近づけば負の無限大に発散するからである。最近発見されたゼロ除算、ゼロで割ることは、その関数値をゼロと解釈すれば良いという簡単なことを言っていて、ゼロ除算はそれを定義とすれば、ゼロ除算は 現代数学の中で未知の世界を拓くと述べてきた。しかし、これは誰でも直感するように、値ゼロは、 原点の周りの値の平均値であることを知り、この定義は自然なものであると 発見初期から認識されてきた。ところが、他方、極めて具体的な解析関数 W = e^{1/z} = 1 + 1/z + 1/2!z^2 + 1/3!z^3 +……. の点 z=0 における値がゼロ除算の結果1であるという結果に接して、人は驚嘆したものと考えられる。複素解析学では、無限位数の極、無限遠点の値を取ると考えられてきたからである。しかしながら、上記の考え、平均値で考えれば、値1をとることが 明確に分かる。実際、原点のコーシー積分表示をこの関数に適用すれば、値1が出てくることが簡単に分かる。そもそも、コーシー積分表示とは 関数の積分路上(簡単に点の周りの円周上での、 小さな円の取り方によらずに定まる)で平均値を取っていることに気づけば良い。
そこで、一般に関数値とは、考えている点の周りの平均値で定義するという原理を考える。
解析関数では 平均値が上手く定義できるから、孤立特異点で、逆に平均値で定義して、関数を拡張できる。しかし、解析的に延長されているとは言えないことに注意して置きたい。 連続関数などは 平均値が定義できるので、関数値の概念は 今までの関数値と同じ意味を有する。関数族では 平均値が上手く定義できない場合もあるが、そのような場合には、平均値のいろいろな考え方によって、関数値の意味が異なると考えよう。この先に、各論の問題が派生する。
以 上
Reality of the Division by Zero $z/0=0$
http://www.ijapm.org/show-63-504-1.html
再生核研究所声明262 (2015.12.09) 宇宙回帰説 ― ゼロ除算の拓いた世界観
最近展開しているゼロ除算が、新しい世界観を示しているのは 大変興味深い。直線とは一体どうなっているだろうか.空間とはどのようになっているだろうか。これについて、現代人は、双方向にどこまでも どこまでも 続いている直線を想像するであろう。限りなく広がった平面や空間である。ところが 立体射影によって 平面全体を球面上に1対1に写せば、全平面は 球面から北極を除いた球面上に1対1にきちんと写るから、無限に広がる 全平面の全貌が捉えられる。ところが平面上には存在しない想像上の点 それはあらゆる方向に限りなく遠くに存在する無限遠点の導入によって、その点を球面の欠けた1点北極に対応させれば、無限遠点を含めた平面全体は 球面全体と1対1にきちんと対応する。
このような対応で 平面上の円や直線全体は 球面上では共に円に対応するという美しい対応になり、平面上の直線は 球面上では、北極(無限遠点)を通る円に写ると、直線と円の区別は 球面上では不要になる。また、平面上の平行線とは 無限遠点で 角度ゼロで交わっている(接している)と平面上の構造がよく見えて、無限遠点を含めての平面の全構造が 捉えられる。このように、考えると、直線とは、球面上では北極を通る円、平面上では無限遠点を通る直線となる。この構造は、直線を1方向にどこまでも, どこまでも進めば、無限遠点を 通って、逆方向から戻ってくるという、永劫回帰の思想をちょうど実現している。それは、球面上では、 円を繰り返し回ることを意味する。 その様は 何もかも すっかり良く見える。
これが、従来100年以上も続いた世界観で、関数y=x やW=zは 無限遠点に近づけば、それらの像も無限遠点に近づいていると考えるだろう。 関数y=x の値は正方向にどんどん行けば、どんどん大きくなると考えるだろう。
しかるに、ゼロ除算1/0=0は、それらの関数は無限遠点にいくらでも近づくと 無限遠点にいくらでも近づくが、無限遠点自身では、突然ゼロになっていることが 幾何学的にも確認された。上記、北極は 実は原点ゼロに一致しているという。
話しを簡単にするために、 関数y=x を考えよう。右に行けば、プラス無限に、負の方向左に行けば 負の無限に限りなく近づくは 従来通りである。ところが、ゼロ除算では いずれの方向でも上記無限遠点では 値ゼロをきちんと取っているという。ゼロ除算の数学では、どんどん、増加した先、突然、ゼロ、原点に戻っているという。また、円でも球面でも半径Rをどんどん大きくすると、当然、円の面積や球の体積はどんどん限りなく大きくなるが、半径が無限のとき、突然、それらはゼロになるという。それらの理由も数学ばかりではなく、幾何学的にも明確に見えている。
この数学的な事実は、我々の世界、宇宙がどんどん拡大して行くと突然、ゼロに帰するということを暗示させている。 ― これは 宇宙回帰説を意味しているようである。
これは、ユニバースの普遍的な現象、どんどん進んだ先が、元に突然戻る原理を示しているようである。
そもそも人生とは如何なるものか。― よくは分からないが、事実として、生まれて、どんどん物心がついて、人間として精神活動が活発化して、多くは本能原理によって生かされて、そして、突然元に戻ることを意味しているようである。このことを深く捉えられれば、世界がよりよく観え、悟りの境地に達する大きなヒントを得ることができるだろう。
ここでは ゼロ除算の帰結として、宇宙回帰説、ユニバースの回帰説を唱えたい。この考えでは、どんどん進めば、突然元に戻るという原理を述べている。珠算における 御破算で願いましては で 再び始めることを想起させる。これは、また、reset と同様であると考えられる。
以 上
再生核研究所声明296(2016.05.06) ゼロ除算の混乱
ゼロ除算の研究を進めているが、誠に奇妙な状況と言える。簡潔に焦点を述べておきたい。
ゼロ除算はゼロで割ることを考えることであるが、物理学的にはアリストテレス、ニュートン、アンシュタインの相当に深刻な問題として、問題にされてきた。他方、数学界では628年にインドで四則演算の算術の法則の確立、記録とともに永年問題とされてきたが、オイラー、アーベル、リーマン達による、不可能であるという考えと、極限値で考えて無限遠点とする定説が永く定着してきている。
ところが数学界の定説には満足せず、今尚熱い話題、問題として、議論されている。理由は、ゼロで割れないという例外がどうして存在するのかという、素朴な疑問とともに、積極的に、計算機がゼロ除算に出会うと混乱を起こす具体的な懸案問題を解消したいという明確な動機があること、他の動機としてはアインシュタインの相対性理論の上手い解釈を求めることである。これにはアインシュタインが直接言及しているように、ゼロ除算はブラックホールに関係していて、ブラックホールの解明を意図している面もある。偶然、アインシュタイン以後100年 実に面白い事件が起きていると言える。偶然、20年以上も考えて解明できたとの著書さえ出版された。― これは、初めから、間違いであると理由を付けて質問を送っているが、納得させる回答が無い。実名を上げず、具体的に 状況を客観的に述べたい。尚、ゼロ除算はリーマン仮説に密接に関係があるとの情報があるが 詳しいことは分からない。
1: ゼロ除算回避を目指して、新しい代数的な構造を研究しているグループ、相当な積み重ねのある理論を、体や環の構造で研究している。例えて言うと、ゼロ除算は沢山存在するという、考え方と言える。― そのような抽象的な理論は不要であると主張している。
2:同じくゼロ除算回避を志向して 何と0/0 を想像上の数として導入し、正、負無限大とともに数として導入して、新しい数の体系と演算の法則を考え、展開している。相当なグループを作っているという。BBCでも報じられたが、数学界の評判は良くないようである。― そのような抽象的な理論は不要であると主張している。
3:最近、アインシュタインの理論の専門家達が アインシュタインの理論から、0/0=1, 1/0=無限 が出て、ゼロ除算は解決したと報告している。― しかし、これについては、論理的な間違いがあると具体的に指摘している。結果も我々の結果と違っている。
4:数学界の永い定説では、1/0 は不可能もしくは、極限の考え方で、無限遠点を対応させる. 0/0 は不定、解は何でも良いとなっている。― 数学に基本的な欠落があって、ゼロ除算を導入しなければ数学は不完全であると主張し、新しい世界観を提起している。
ここ2年間の研究で、ゼロ除算は 何時でもゼロz/0=0であるとして、 上記の全ての立場を否定して、新しい理論の建設を進めている。z/0 は 普通の分数ではなく、拡張された意味でと初期から説明しているが、今でも誤解していて、混乱している人は多い、これは真面目に論文を読まず、初めから、問題にしていない証拠であると言える。
上記、関係者たちと交流、討論しているが、中々理解されず、自分たちの建設している理論に固執しているさまがよく現れていて、数学なのに、心情の問題のように感じられる微妙で、奇妙な状況である。
我々のゼロ除算の理論的な簡潔な説明、それを裏付ける具体的な証拠に当たる結果を沢山提示しているが、中々理解されない状況である。
数学界でも永い間の定説で、初めから、問題にしない人は多い状況である。ゼロ除算は算数、ユークリッド幾何学、解析幾何学など、数学の基本に関わることなので、この問題を究明、明確にして頂きたいと要請している:
再生核研究所声明 277(2016.01.26):アインシュタインの数学不信 ― 数学の欠陥
再生核研究所声明 278(2016.01.27): 面白いゼロ除算の混乱と話題
再生核研究所声明279(2016.01.28) : ゼロ除算の意義
再生核研究所声明280(2016.01.29) : ゼロ除算の公認、認知を求める
我々のゼロ除算について8歳の少女が3週間くらいで、当たり前であると理解し、高校の先生たちも、簡単に理解されている数学、それを数学の専門家や、ゼロ除算の専門家が2年を超えても、誤解したり、受け入れられない状況は誠に奇妙で、アリストテレスの2000年を超える世の連続性についての固定した世界観や、上記天才数学者たちの足跡、数学界の定説に まるで全く嵌っている状況に感じられる。
以 上
考えてはいけないことが、考えられるようになった。
説明できないことが説明できることになった。
Matrices and Division by Zero z/0 = 0















































