こんにちは!
じんです!!
今回は
苦手な人と得意な人で
差がついてしまう
物理のお話です。
これを読んでいるあなたは
物理は難しい...
と思っていることでしょう。
しかし難しいと
思っているままでは
なかなか伸ばせませんし、
物理が足を引っ張ることになれば
そのまま不合格への道を
辿ってしまうことに
なるかもしれません。
物理が苦手なせいで
志望校を諦める...
なんてことには
なりたくないですよね
そのためにも物理の事を
知っていきましょう。
まず最初に言ったように
物理は
得意不得意で
かなり差がつきます!
得意な人は
かなり高得点を
取ることができますし、
苦手な人は
ほんの少しの点しか
取れない...
なんてことも珍しくありません。
このような事になるのは
物理の入試問題の仕組み上
なので仕方ないのです。
その仕組みとは
物理はおよそ、大問が三つ前後で
出題されることが多いですが、
小問が独立して
あるわけではなく
前問の流れで解く、
前問に関連した問題
というのが多いのです。
つまり、簡単な例をあげると
一つの大問の中の小問は
1,2,3,4,5,6まであったとしても、
3が解けなかったら
あとの4~6は解けない
といったことがあります。
かいつまんで
解ける問題を解くというような
戦略が使えない事が多いです。
ですから、物理は
苦手なままだと苦労しますし、
何より得意にすれば
苦手な人と差をつけて
大幅な得点源にもなるのです!
それでは
物理が得意になるには
どうしたらよいのが
ですが、
式の意味の理解を
きっちりとしましょう。
物理ができていない人は
そもそも立式が
出来ていない
あるいは立てた式が
間違えている事が
ほとんどです。
これが表しているのは
基礎がまだ不十分
ということです。
物理は覚えることが
少ないですから
ちゃんと基礎が
理解できているかで
大きな差が出ます。
理解できているか
というか理解の深さでしょうか。
「式の意味を
理解して使っていますか?」
「立てた式の意味を
きっちりと自分で
説明できますか?」
この辺のことを意識して
ほしいと思います。
運動方程式を
例とするなら
Mα=Fの意味は
質量Mの物体が
力Fを受けるとき
その物体には
受けた力に比例した
加速度 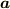 が生じる
が生じる
ですよね。
(解釈の仕方は
他にもありますよ!)
こういう式の意味を
しっかりと理解していること。
そしてそれを
きちんと使えること
つまり
実際に問題を解くときに
立てた運動方程式を
自分で説明できますか
(分かった上で式を
立ててますか?)
ということです。
Mα=F+T であったら
力がFとTで
同じ向きであるから、
右辺はこうなっている
といった感じです。
これは
ごく基本的な例ですから
簡単かもしれませんが
解けなかった問題のときに
こういう風に自分で
説明できるか
確認してみると良いですね!
立式が出来ていない人は
数学と同様で、
何を求める必要があり、
何の式を立てたらいいか
を考えて勉強しましょう!
こういった
些細な事や
些細な理解の差が
問題の出来に
かかわってきます。
物理は理解を
最優先に勉強してください!
このことは意識しないと
忘れがちです。
忘れては
意味がありませんから、
いつでも見れるように、
物理を伸ばすためにも
今すぐ
「物理は式の意味の理解が大事」
とメモをしましょう!!
今すぐですよ!
最後まで読んで頂いて
ありがとうございます!
また次の記事でお会いしましょう!


