これを使ってさっそく遊んでみたい所ですが、そのためには何かデータをでっち上げなければなりません。
今まで出てきたサンプルプログラムでは、GSLの乱数発生器でデータを作っていましたが、多変量の場合は用意されているものが限られます。
正規分布の場合、以下の2変量の乱数発生器が用意されています。
void gsl_ran_bivariate_gaussian (gsl_rng *rng, double sigmax, double sigmay, double rho, double *x, double *y);
この関数では、データ分布についての x軸、y軸方向の標準偏差 σx、σy と、x-y軸方向の相関係数 ρ を入力します。
これで、平均 0、
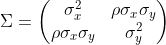
の分散共分散行列に従う2次元の正規乱数を作る事が出来ます。
でも3次元以上の場合は自分で作らないといけないようです。
M次元の多変量正規乱数を作る手順は以下の通り(例えばこちら)。
1.平均 0、分散 1 の標準正規分布に従う M 次元ベクトルを作成
(乱数を M 個引いて一次元配列に突っ込む)。
2.平均ベクトル(M 次元)、分散共分散行列(M 行 M 列)を指定する。
3.分散共分散行列をコレスキー分解し、下三角行列の方を取得。
4.3.の下三角行列に 1.で得られている M 次元ベクトルを掛ける。
これを N 回繰り返せば、N 個の M 変量正規乱数が得られます。
以下の関数群で上記の操作を行います。
ここで、分散共分散行列の指定方法ですが、GSLの2変量のものに準じて
各軸方向の標準偏差
各軸同士の相関係数
を1次元配列で与えるものとします。
例えば3次元の場合
標準偏差 = [σx、 σy、 σz]
相関係数 = [ρxy、 ρxz、 ρyz] <-- 1行目から順に格納!!
を与えた場合、分散共分散行列は

となります。
ここで ρには -1 ~ 1 の値を指定します。
#include <stdio.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_matrix.h>
#include <gsl/gsl_blas.h>
#include <gsl/gsl_linalg.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
/*** 標準正規乱数に従う ndim 次元GSLベクトルを取得 ***/
static gsl_vector *
normal_gaussian_vector (const gsl_rng *r, const size_t ndim)
{
int j;
gsl_vector *v = gsl_vector_alloc (ndim);
// ベクトル v の第 j 成分に標準正規乱数(gsl_ran_gaussian)を格納
for (j = 0; j < ndim; j++) gsl_vector_set (v, j, gsl_ran_gaussian (r, 1.));
return v;
}
/*** 標準偏差 *sigma、相関係数 *rho の分散共分散行列を取得 ***/
static gsl_matrix *
covariance_matrix (const size_t ndim, const double *sigma, const double *rho)
{
int j, l;
gsl_matrix *cov = gsl_matrix_alloc (ndim, ndim);
for (j = 0; j < ndim; j++) {
for (l = j; l < ndim; l++) {
// 対角成分は標準偏差の二乗
if (j == l) gsl_matrix_set (cov, j, j, sigma[j] * sigma[j]);
else {
// 非対角成分は、相関係数 × 標準偏差1 × 標準偏差2
gsl_matrix_set (cov, j, l, rho[j + l - 1] * sigma[j] * sigma[l]);
// 対称行列なので同じ値
gsl_matrix_set (cov, l, j, gsl_matrix_get (cov, j, l));
}
}
}
return cov;
}
/*****************************************************
コレスキー分解
入力の行列 gsl_matrix *cov をコレスキー分解し
下三角行列で上書きする。
*****************************************************/
static void
cholesky_decomp_ltri (gsl_matrix *cov)
{
int j, l;
// 行列 cov を、 cov = L * L^T なる下三角行列(とその転置の積)に分解
// 入力の cov は L と L^T の上三角部分で上書きされる。
// http://www.gnu.org/software/gsl/manual/html_node/Cholesky-Decomposition.html
gsl_linalg_cholesky_decomp (cov);
// 上三角部分を 0 で置き換え、下三角行列にする。
for (j = 0; j < cov->size1; j++) {
for (l = j + 1; l < cov->size2; l++) {
gsl_matrix_set (cov, j, l, 0.);
}
}
return;
}
/*******************************************************************************
多変量正規分布に従う ndim 次元の乱数ベクトルを計算する。
引数
const gsl_rng *rng : gsl乱数
const size_t ndim : 乱数ベクトルの次元
const double *mu : 正規分布の平均ベクトル(ndim 次元)
const double *sigma : 標準偏差(要素数 = ndim 個)
const double *rho : 相関係数(要素数 = ndim * (ndim - 1) / 2 個)
*******************************************************************************/
double *
ran_multivar_gaussian (const gsl_rng *rng, const size_t ndim,
const double *mu, const double *sigma, const double *rho)
{
int j;
// 分散共分散行列
gsl_matrix *cov;
// 標準正規乱数ベクトル
gsl_vector *normal;
// コレスキー分解
gsl_matrix *chol;
// 多変量正規乱数を格納する配列
double *x;
// 多変量正規乱数を格納する配列を指すベクトルの像
gsl_vector_view vx;
// 標準正規乱数ベクトルを取得
normal = normal_gaussian_vector (rng, ndim);
// 標準偏差、相関係数から分散共分散行列を計算
cov = covariance_matrix (ndim, sigma, rho);
// 分散共分散行列をコレスキー分解
cholesky_decomp_ltri (cov);
chol = cov;
/*** 以下で コレスキー分解 x 標準正規乱数ベクトル を計算 ***/
// 計算結果(正規乱数)を格納する配列
x = (double *) malloc (ndim * sizeof (double));
// x を指すベクトルの像を作成
vx = gsl_vector_view_array (x, ndim);
// vx の指す一次元配列 *x に chol x normal の行列×ベクトルの結果を格納
gsl_blas_dgemv (CblasNoTrans, 1., chol, normal, 0., &vx.vector);
gsl_vector_free (normal);
gsl_matrix_free (cov);
// 平均の値だけずらす。
for (j = 0; j < ndim; j++) x[j] += mu[j];
return x;
}/******************************************************************************
テストデータの作成
ndim 次元の ndata 個の多変量正規乱数を作成。
引数
unsigned long int seed : 乱数のseed値
const size_t ndata : データ数
const size_t ndim : 乱数ベクトルの次元
const double *mu : 正規分布の平均ベクトル(ndim 次元)
const double *sigma : 標準偏差(要素数 = ndim 個)
const double *rho : 相関係数(要素数 = ndim * (ndim - 1) / 2 個)
*******************************************************************************/
double *
test_data (unsigned long int seed, const size_t ndata, const size_t ndim,
const double *mu, const double *sigma, const double *rho)
{
int i, j;
double *data;
// 乱数の初期化
const gsl_rng *r = gsl_rng_alloc (gsl_rng_default);
// 乱数の種を設定
gsl_rng_set (r, seed);
data = (double *) malloc (ndata * ndim * sizeof (double));
for (i = 0; i < ndata; i++) {
// 乱数ベクトルを取得
double *x = ran_multivar_gaussian (r, ndim, mu, sigma, rho);
// それを i 番(行)目のデータとして格納
for (j = 0; j < ndim; j++) data[i * ndim + j] = x[j];
free (x);
}
return data;
}
上の関数
double *test_data ()
で、指定された平均、分散共分散に従う多変量正規乱数が取得できるはず(汗)です。
この関数で得られたデータを出力するために下の関数を用意しました。
これで row major で1次元配列に格納された行列を FILE *stream に出力できます。
/*** row major で1次元配列に格納された行列を出力 ***/
void
fprintf_row_major_array (FILE *stream, const size_t size1, const size_t size2,
const double *data, const char *format)
{
int i, j;
for (i = 0; i < size1; i++) {
for (j = 0; j < size2; j++) {
int index = i * size2 + j;
fprintf (stream, format, data[index]);
if (j < size2 - 1) fprintf (stream, "\t");
}
fprintf (stream, "\n");
}
return;
}
ところで、上の関数群でほんとに正規分布に従う乱数が得られているのか気になりますね・・・
それを確かめるため、こちらでも話題になっているQ-Qプロットで確かめてみましょう。
これは、正規乱数のマハラノビス距離が自由度 ndim のカイ二乗分布に従う(例えばごりら)事から、得られたデータのマハラノビス距離とカイ二乗分布のパーセンタイル(の理論値)とを比較するものです。
/*** 以下は、得られたデータが本当に正規分布になってるか確認する為の物 ***/
#include <gsl/gsl_statistics.h>
#include <gsl/gsl_sort.h>
#include <gsl/gsl_cdf.h>
/*** データから平均ベクトルを求める ***/
static gsl_vector *
sample_mean_vector (const size_t ndata, const size_t ndim, const double *data)
{
int j;
// 平均ベクトル
gsl_vector *mu = gsl_vector_alloc (ndim);
// データ double *data を指すベクトルの像
gsl_matrix_const_view y = gsl_matrix_const_view_array (data, ndata, ndim);
// 行列 y (data) の j 列目を格納。その平均は、平均ベクトルの j 成分
gsl_vector *xj = gsl_vector_alloc (ndata);
for (j = 0; j < ndim; j++) {
gsl_matrix_get_col (xj, &y.matrix, j);
// xj の平均を mu の j 番目要素に代入
gsl_vector_set (mu, j, gsl_stats_mean (xj->data, 1, ndata));
}
gsl_vector_free (xj);
return mu;
}
/*** データから分散共分散行列を求める ***/
static gsl_matrix *
sample_covariance_matrix (const size_t ndata, const size_t ndim, const double *data)
{
int j, l;
// 分散共分散行列
gsl_matrix *cov = gsl_matrix_alloc (ndim, ndim);
// データ double *data を指すベクトルの像
gsl_matrix_const_view y = gsl_matrix_const_view_array (data, ndata, ndim);
// 行列 y (data) の j 列目を格納
gsl_vector *xj = gsl_vector_alloc (ndata);
// 行列 y (data) の l 列目を格納
gsl_vector *xl = gsl_vector_alloc (ndata);
for (j = 0; j < ndim; j++) {
gsl_matrix_get_col (xj, &y.matrix, j); // 行列 y (data) の j 列目
for (l = j; l < ndim; l++) {
gsl_matrix_get_col (xl, &y.matrix, l); // 行列 y (data) の l 列目
// xj と xl の共分散を cov の j 行 l 列目に代入
gsl_matrix_set (cov, j, l,
gsl_stats_covariance (xj->data, 1, xl->data, 1, ndata));
// cov は対称行列
if (j != l) gsl_matrix_set (cov, l, j, gsl_matrix_get (cov, j, l));
}
}
gsl_vector_free (xl);
gsl_vector_free (xj);
return cov;
}
/********************************************
各データのマハラノビス距離を計算。
モホロビチッチに次ぐ読みにくい名前
********************************************/
double *
mahalanobis_distance (const size_t ndata, const size_t ndim, const double *data)
{
int i, j;
gsl_vector *mu;
int s;
gsl_matrix *cov;
gsl_matrix *icov;
gsl_permutation *p;
// 各データのマハラノビス距離を格納
double *res = (double *) malloc (ndata * sizeof (double));
gsl_matrix_const_view y = gsl_matrix_const_view_array (data, ndata, ndim);
// データから平均ベクトル、分散共分散行列を計算
mu = sample_mean_vector (ndata, ndim, data);
cov = sample_covariance_matrix (ndata, ndim, data);
// LU分解して共分散行列の逆行列を求める。前に見た気がする。
p = gsl_permutation_alloc (ndim);
gsl_linalg_LU_decomp (cov, p, &s);
// 共分散行列の逆行列
icov = gsl_matrix_alloc (ndim, ndim);
gsl_linalg_LU_invert (cov, p, icov);
gsl_permutation_free (p);
gsl_matrix_free (cov);
for (i = 0; i < ndata; i++) {
double s2; // i 番目データのマハラビノス距離
gsl_vector *xm; // xm = x_i - μ
gsl_vector *s1; // s1 = Σ^-1 * xm 安易な名前。
// xm は(i 番目データベクトル)- (平均ベクトル)
xm = gsl_vector_alloc (ndim);
gsl_matrix_get_row (xm, &y.matrix, i);
gsl_vector_sub (xm, mu);
// s1 = Σ^-1 * xm
s1 = gsl_vector_alloc (ndim);
gsl_blas_dgemv (CblasNoTrans, 1., icov, xm, 0., s1);
// s2 = xm^T * Σ^-1 * xm
gsl_blas_ddot (s1, xm, &s2);
gsl_vector_free (s1);
gsl_vector_free (xm);
res[i] = s2;
}
gsl_matrix_free (icov);
return res;
}
/*** Q-Q プロットを出力して直線に近ければ合格? ***/
void
fprintf_qqplot (FILE *stream, const size_t ndata, const size_t ndim, double *s2)
{
int i;
// まずソート
gsl_sort (s2, 1, ndata);
for (i = 0; i < ndata; i++) {
// p * 100 パーセンタイル点
double p = (double) i / (double) ndata;
// カイ二乗分布の p * 100 パーセンタイル値
// GSL・カイ二乗分布の累積密度関数逆関数を使用
double chisq_percentile_p = gsl_cdf_chisq_Pinv (p, ndim);
fprintf (stream, "%f\t%f\t%f\n", p, chisq_percentile_p, s2[i]);
}
return;
}
以上の関数群を使って、100個の3次元の正規乱数を作るメイン関数のサンプルが下です。
int
main (void)
{
size_t ndata = 100;
size_t ndim = 3;
double mu[3] = {0., 0., 0.};
double sigma[3] = {2., 1., 5.};
double rho[3] = {0.3, -0.2, 0.3};
double *data = test_data (100, ndata, ndim, mu, sigma, rho);
// ヘンテコリンな仕様ですが gsl_matrix_fprintf に準じています。。。
fprintf_row_major_array (stdout, ndata, ndim, data, "%f");
{
double *s2 = mahalanobis_distance (ndata, ndim, data);
FILE *fp = fopen ("qqplot.res", "w");
if (fp != NULL) {
fprintf_qqplot (fp, ndata, ndim, s2);
fclose (fp);
}
free (s2);
}
return 0;
}
一応、上の物をそのままファイルにコピペして
$ gcc -g -o hoge hogehoge.c $(pkg-config gsl --libs --cflags)
でコンパイルできるはずです。
あ、windowsではどうするのか知りません(汗
GSLでググってください(涙
とにかく、実行すると、標準出力に正規乱数が出力されます。
同時に qqplot.res というファイルが出来上がるので、それの 2 フィールド目 v.s. 3フィールド目 をプロットしたQ-Qプロットが直線になっていれば合格、というところでしょう。
で、下が上の main 関数で出力された正規乱数と Q-Qプロットの結果です。
Q-Qプロットのほうは、まぁ直線なんでしょうかね?
あんまり自信が無いんですが(汗)なんか間違いがあったら教えてください・・・

