式(1)
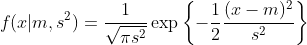
と書けます。
これは、この正規分布から値 x が生じる確率を表します。
また、この正規分布から独立に n 個のデータ (x1, x2, ... xn) を引く確率(同時確率)は
式(2)

となります。
この時上の式は、分布のバラメータ m と s^2 が既知で、データ x はユーザが与える変数となっています。
でも逆に、データ x が既知で分布のパラメータが未知の場合を考えます。
例えば
「ランダムノイズと思われるデータが観測されたんだけど、ノイズを発生させる確率分布の平均・分散を求めたい」
なんて場合には、データ x は既に得られた既知の量となるのに対し、m や s^2 は観測者が何らかの方法で決めなければいけない変数となります。
この時(1)や(2)の式は、観測者が決めた m や s^2 の値がデータ分布に対しどのくらい尤も(もっとも)らしいかを表す関数となり、「尤度関数」と呼ばれます。
関数の形は全く変わらないけど、どれが未知でどれが既知かで見方が変わる、つまり(1)、(2)式で計算される値の意味が変わるんですね。
例えば未知の正規分布からデータが一個得られたとしましょう。
そのたった一個のデータとして、出現確率が低い値が得られる事はごく稀でしょう。
日曜にパチンコ行ってたまたま座った台で、一発目の確変で大当たりを引く位稀でしょう。
当たったらウハウハですが。。。
できる事なら先週スッた1万5千円取り返したい・・・(涙
それより、一個だけ得られたデータが正規分布の平均に近い(出る確率の高い値である)事の方がよっぽど尤もらしいでしょう。
ここで、得られたデータ x の値を平均値に持つ場合、つまり m=x とした場合で(1)式を計算すると、同じ分散 s^2 の値で比較するとその時の値が最も大きくなります。
例えば x=1 だったとしたら、(1)の式で
f(x=1 | m=1, s^2)
が、同じ分散 s^2 の値で比較すると最も大きくなります。
尤度関数の値が尤もらしさを表す、つまり尤度関数の値が大きい=尤もらしい、小さい=尤もらしくない、と考えれば上の例は
「一個だけ得られたデータが、正規分布の平均に近い事の方がよっぽど尤もらしい」
という直観と合いますね~
次にデータが2個の場合を考えましょう。
ここで、一つ目のデータ x1 の値がむちゃくちゃ出やすいのに対し二番目のデータ x2 の値がメチャ出にくい、なんて事はバランスが悪そうですね。
そんな状況を(2)式に置き換えて、一番目のデータ x1 を平均に持つ下の図の様な分布を考えます。
f(x1 | m = x1, s^2) は大きくなりますが二番目のデータ x2 が出る事は稀、つまり f(x2 | m = x1, s^2) が小さくなるので(2)式は小さな値になってしまいます。
それよりはどっちの値もそこそこ出やすい、という無難な状況を考えた方がよさげです。
(2)式でも、平均 m が2つのデータの中間辺りにあり、x1、x2 どちらの値もそこそこ出やすい分布を考えた方が(2)式の値はずっと大きくなります。
バランスが大切ですね。おとなのもびっと。
こんな風に(例として説得力があるかは不明ですが・・・)、尤度関数はユーザが選んだ分布、つまり m とか s^2 とかのパラメータの値が、実際に得られたデータの分布に対してどのくらい尤もらしいかを示す指標を与えてくれます。
最も尤度関数(1)、(2)式の値を大きくするパラメータを最尤パラメータと呼びますが、例えば平均 m の最尤パラメータは下の尤度関数のlog、対数尤度に対する尤度方程式を解く事で得られます。
式(3)
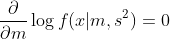
分散についても同様に
式(4)
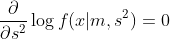
を解いて得られます。
ちなみに正規分布の場合、平均の最尤解は標本平均、分散は標本平均から測った分散になります。
で、懸案のAICについてですが、前回の最後にK-L情報量(の近似値)は
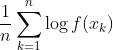
の対数尤度関数を最大にするモデルで最小になる、という事でしたが、その「対数尤度を最大にするモデル(のパラメータ)」こそ、(3)、(4)式を解いて得られる最尤パラメータである、という事になります。
