[答1837] 直角三角形内の正三角形
∠B=90゚,AB=6 ,BC=9√3 である △ABCの、辺AB上に点P,辺BC上に点Q,辺CA上に点Rを
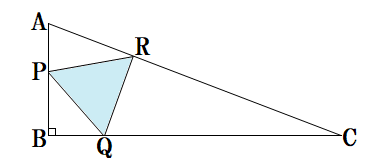
とって、正三角形PQRを描き、その1辺を L とするとき、L の最小値は?
[解答1]
座標平面上で A(0,6),B(0,0),C(9√3,0),P(0,p),Q(q,0) とします。
複素数平面上で、有向線分QPを表す複素数 ip-q を -60゚ 回転すると、
(ip-q)(1-i√3)/2=(ip-q+p√3+iq√3)/2=(-q+p√3)/2+i(p+q√3)/2 だから、
Rを表す複素数は、(-q+p√3)/2+i(p+q√3)/2+q=(p√3+q)/2+i(p+q√3)/2 、
R((p√3+q)/2,i(p+q√3)/2) です。
直線ACは、x/(9√3)+y/6=1 で、直線AC上にRがあるから、
(p√3+q)/(18√3)+(p+q√3)/12=1 、2(p√3+q)+(3√3)(p+q√3)/12=36√3 、
(5√3)p+11q=36√3 です。
コーシー・シュワルツの不等式より、{(5√3)2+112}(p2+q2)≧{(5√3)p+11q}2 、
196L2≧(36√3)2 、14L≧36√3 、L≧(18√3)/7 です。
等号が成り立つのは、p:q=5√3:11 のときで、p=(5√3)k,q=11k とおけば、
(5√3)p+11q=36√3 より、75k+121k=36√3 、196k=36√3 、k=(9√3)/49 だから、
最小値は (18√3)/7 、p=135/49,q=(99√3)/49 のときです。
[解答2]
座標平面上で A(0,6),B(0,0),C(9√3,0),R(X,Y),∠PQB=θ とします。
∠RQC=120゚-θ,∠BPQ=90゚-θ,∠APR=30゚+θ 、
X/L=sin(30゚+θ)=sin30゚cosθ+cos30゚sinθ 、2X/L=cosθ+(√3)sinθ 、
Y/L=sin(120゚-θ)=sin120゚cosθ-cos120゚sinθ 、2Y/L=(√3)cosθ+sinθ 、
直線ACは、x/(9√3)+y/6=1 、18√3=2x+(3√3)y 、(36√3)/L=2(2x/L)+(3√3)(2y/L) 、
Rは直線AC上にあるので、
(36√3)/L=2(2X/L)+(3√3)(2Y/L)=2{cosθ+(√3)sinθ}+(3√3){(√3)cosθ+sinθ}
=11cosθ+(5√3)sinθ=14cos(θ-α) 、
( ただし、αは ベクトル(11,5√3)とx軸の正方向のなす角で鋭角 )
よって、θ=α のとき (36√3)/L の最大値が 14 になり、
L/(36√3) の最小値が 1/14 、L の最小値は (36√3)/14=(18√3)/7 です。
.

