検討課題:霊的宇宙をどう説明するのか:新コスモス論(ポスト占星術的宇宙)へ向けて
本問題は、実に長い間の懸案であるが、未だ決定打となる仮説が出てこないのである。私は、西洋占星術の基本的な概念を肯定しているが、その日の占い・運勢のようなものは信じない。
つまり、星座(正しくは、宮)と性格との相関性をみとめているのであるが、その「科学」的原理が説明できないのである。
単に迷信と切り捨てるのは、容易であるが、占星術が経験知に合致する側面を捨て去ることになる。
シュタイナーの体論から言えば、アストラル体(感情、欲望体)と占星術は関係すると考えられる。
それは、思うに、MP(原点)に存する様態のように思える。
ここで作業仮説として、凸iを火、凹iを水、-1を地、+1を風とする。つまり、四大(地水火風)をそう設置してみる。
そうすると、第一象限には、風象星座(双子座、天秤座、水瓶座)、第二象限には、火象星座(牡羊座、獅子座、射手座)、第三象限には、地象星座(牡牛座、乙女座、山羊座)、第四象限には、水象星座(蟹座、蠍座、魚座)を配置できるのかもしれない。
もっとも、基軸は、風象星座の場合は、+1であり、火象星座の場合は、凸iであり、地象星座の場合は、-1であり、水象星座の場合は、凹iである。
そして、各象限を三等分(30度で区分)して、基軸から数えることにすると、第一象限の第一区分は水瓶座、第二区分は、天秤座?、第三区分は双子座?、そして、第二象限の第一区分は、獅子座?、第二区分は、牡羊座?、第三区分は射手座?、そして、第三象限の第一区分は、牡牛座、第二区分は、山羊座?、第三区分は、乙女座?、そして、第四象限の第一区分は、蠍座?、第二は蟹座?、第三は魚座?だろうか。
とまれ、そう作業仮説すると、誕生のとき、各個人の魂(個魂)は、ある陰陽双極子の様態をもっていて、それが、どの象限に属するかで、誕生日が異なるということではないだろうか。今日は、9月4日で、乙女座になる。乙女座の人は、陰陽双極子が誕生に際して、第三象限の第三区分に存していたということになる。
しかしながら、これは、性格(だけではないが)に関わることであり、個の本性ではない。個の本性は、霊的なものであり、先に述べたように、個霊性である。
それは、超越界、超越円に属するものと考えられる。
<無双PS原理三次元世界:Ver4.1>
虚軸y軸:陽・凸i・時間形式・自己
/
超越軸z軸:太極・霊界 /
| /
| /
| /
Ⅱ:物質認識 | / Ⅰ:頭
| /
| /
-1__←重力波_MP・胸_電磁波⇒_+1実軸x軸
地・自我 / | 天・個
/ |
Ⅲ:肚 / | Ⅳ:精神認識(魂認識)
/ |
/ |
陰・凹i・空間形式 |
・他者 |

直交座標系による平面上の点の座標と四つの象限

http://chaos2ch.com/archives/3095318.html
参照:
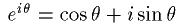
(e:自然対数)
この式はオイラーの公式と呼ばれています。この式を知っていると計算の見通しが良くなるので高校生でも知っておくと良いと思います。そこで、オイラーの公式を複素数に使いオイラーの公式の使い方について考えてみます。
複素数は、
Z=|Z|(cosθ+i sinθ)
と極座標(距離と角度)の形式で表すことができます。
このとき、Z1とZ2の積を考えると、
Z1×Z2=|Z1|(cos(θ1)+i sin(θ1))|Z2|(cos(θ2)+isin(θ2))
=|Z1||Z2|(cos(θ1+θ2)+i sin(θ1+θ2))
となります。
この式の図形的意味を考えると、
(Z1にZ2を掛ける)=(Z1を|Z2|倍に拡大)+(Z1をθ2回転)
というように解釈できます(これは複素数を図形的に考えるときに重要です)。
さて、ここからオイラーの公式を使うと役に立つ理由 を説明します。
上で積を考えたときに,計算で気になるのは、
(cos(θ1)+i sin(θ1))×(cos(θ2)+isin(θ2)) =cos(θ1+θ2)+i sin(θ1+θ2)
の部分です。 この式は、本来なら加法定理を利用して整理すべきものですよね。
しかし,オイラーの公式を使えば、
(cos(θ1)+i sin(θ1))×(cos(θ2)+i sin(θ2)) =(eiθ1)×(eiθ2)
=ei(θ1+θ2) (ea×eb=ea+bを使った)
=cos(θ1+θ2)+i sin(θ1+θ2) (オイラーの公式を使った)
このように指数関数の性質を使い簡単に計算することができます (加法定理の計算を指数関数の積にすることができた)。
また,オイラーの公式を使えばド・モアブルの式は、 (eiθ)n = ei nθ という,指数関数の性質である(ea)b=eabのことを言っているだけだということがわかります。
最後にポイントをまとめます。
<研究>三角関数を指数関数であらわす
オイラーの公式より、
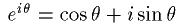 -(1)
-(1)
オイラーの公式の複素共役を取ると、
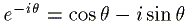 -(2)
-(2)
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
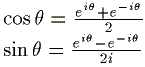
よって、三角関数は指数関数で表された。
http://ameblo.jp/neomanichaeism/entry-11344606343.html
つまり、星座(正しくは、宮)と性格との相関性をみとめているのであるが、その「科学」的原理が説明できないのである。
単に迷信と切り捨てるのは、容易であるが、占星術が経験知に合致する側面を捨て去ることになる。
シュタイナーの体論から言えば、アストラル体(感情、欲望体)と占星術は関係すると考えられる。
それは、思うに、MP(原点)に存する様態のように思える。
ここで作業仮説として、凸iを火、凹iを水、-1を地、+1を風とする。つまり、四大(地水火風)をそう設置してみる。
そうすると、第一象限には、風象星座(双子座、天秤座、水瓶座)、第二象限には、火象星座(牡羊座、獅子座、射手座)、第三象限には、地象星座(牡牛座、乙女座、山羊座)、第四象限には、水象星座(蟹座、蠍座、魚座)を配置できるのかもしれない。
もっとも、基軸は、風象星座の場合は、+1であり、火象星座の場合は、凸iであり、地象星座の場合は、-1であり、水象星座の場合は、凹iである。
そして、各象限を三等分(30度で区分)して、基軸から数えることにすると、第一象限の第一区分は水瓶座、第二区分は、天秤座?、第三区分は双子座?、そして、第二象限の第一区分は、獅子座?、第二区分は、牡羊座?、第三区分は射手座?、そして、第三象限の第一区分は、牡牛座、第二区分は、山羊座?、第三区分は、乙女座?、そして、第四象限の第一区分は、蠍座?、第二は蟹座?、第三は魚座?だろうか。
とまれ、そう作業仮説すると、誕生のとき、各個人の魂(個魂)は、ある陰陽双極子の様態をもっていて、それが、どの象限に属するかで、誕生日が異なるということではないだろうか。今日は、9月4日で、乙女座になる。乙女座の人は、陰陽双極子が誕生に際して、第三象限の第三区分に存していたということになる。
しかしながら、これは、性格(だけではないが)に関わることであり、個の本性ではない。個の本性は、霊的なものであり、先に述べたように、個霊性である。
それは、超越界、超越円に属するものと考えられる。
<無双PS原理三次元世界:Ver4.1>
虚軸y軸:陽・凸i・時間形式・自己
/
超越軸z軸:太極・霊界 /
| /
| /
| /
Ⅱ:物質認識 | / Ⅰ:頭
| /
| /
-1__←重力波_MP・胸_電磁波⇒_+1実軸x軸
地・自我 / | 天・個
/ |
Ⅲ:肚 / | Ⅳ:精神認識(魂認識)
/ |
/ |
陰・凹i・空間形式 |
・他者 |

直交座標系による平面上の点の座標と四つの象限

http://chaos2ch.com/archives/3095318.html
12の星座の性格・星占い
西洋占星術(星占い)では、星座と星をもとに、主として性格や才能、資質を明らかにします。相手をどう理解し、どのように接したらよいのかといった、人間関係の問題、自分の欠点をどう受けとめたらよいのかといった、自分に関する問題、職業選択、人生の進路、 ...参照:
陰陽双極子の方程式と計算
テーマ:無双PS原理今日も簡単に述べるに留める。
先に次のように述べた。
「Ⅰ*Ⅱ=f(θ)*f(θ+π)=〔icosθ+jsinθ〕*〔icos(θ+π)+jsin(θ+π)〕(ただし、θ=nπである。)
これを、霊/気転換方程式と作業仮説的に呼んでおこう。」
これは、超越軸と虚軸の形成する平面における方程式である。
便宜上に簡単にするために、これを虚軸と実軸によるガウス平面に降ろして考える。そうすると、
Ⅰ*Ⅱ=f(θ)*f(θ+π)=〔cosθ+isinθ〕*〔cos(θ+π)+isin(θ+π)〕(ただし、θ=nπである。)
しかし、これは、より簡潔になる。
Ⅰ*Ⅱ=f(θ)*f(θ+π)=〔cosθ+isinθ〕*〔cos(θ+π)+isin(θ+π)〕=cos(2θ+π)*isin(2θ+π)(ただし、θ=nπである。)
これは言い換えると、ガウス平面上の単位円の周囲における、言わば、双極子である。
具体的に見ると、θ=π/6=30°のとき、
Ⅰ・Ⅱ=cos(4π/3)*isin(4π/3)=-1/2-i√3/2
となる。
これは、第三象限に属するが、これが何を意味するのかは、おいておく。
追記:以下にあるようオイラーの公式を使えば、より簡潔になるだろう。
追記2:解答値の-1/2-i√3/2であるが、これを第三象限に属すると述べたが、実軸-1/2、虚軸-√3/2に位置する単位円上の点である。
参考:
オイラーの公式の使い方
オイラーの公式の使い方
大学に入ると次のような式を学びます。(e:自然対数)
この式はオイラーの公式と呼ばれています。この式を知っていると計算の見通しが良くなるので高校生でも知っておくと良いと思います。そこで、オイラーの公式を複素数に使いオイラーの公式の使い方について考えてみます。
複素数は、
Z=|Z|(cosθ+i sinθ)
と極座標(距離と角度)の形式で表すことができます。
このとき、Z1とZ2の積を考えると、
Z1×Z2=|Z1|(cos(θ1)+i sin(θ1))|Z2|(cos(θ2)+isin(θ2))
=|Z1||Z2|(cos(θ1+θ2)+i sin(θ1+θ2))
となります。
この式の図形的意味を考えると、
(Z1にZ2を掛ける)=(Z1を|Z2|倍に拡大)+(Z1をθ2回転)
というように解釈できます(これは複素数を図形的に考えるときに重要です)。
さて、ここからオイラーの公式を使うと役に立つ理由 を説明します。
上で積を考えたときに,計算で気になるのは、
(cos(θ1)+i sin(θ1))×(cos(θ2)+isin(θ2)) =cos(θ1+θ2)+i sin(θ1+θ2)
の部分です。 この式は、本来なら加法定理を利用して整理すべきものですよね。
しかし,オイラーの公式を使えば、
(cos(θ1)+i sin(θ1))×(cos(θ2)+i sin(θ2)) =(eiθ1)×(eiθ2)
=ei(θ1+θ2) (ea×eb=ea+bを使った)
=cos(θ1+θ2)+i sin(θ1+θ2) (オイラーの公式を使った)
このように指数関数の性質を使い簡単に計算することができます (加法定理の計算を指数関数の積にすることができた)。
また,オイラーの公式を使えばド・モアブルの式は、 (eiθ)n = ei nθ という,指数関数の性質である(ea)b=eabのことを言っているだけだということがわかります。
最後にポイントをまとめます。
<Point> オイラーの公式のメリット
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|e iθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
Z=|Z|(cosθ+i sinθ)をオイラーの公式を使いZ=|Z|e iθと表すと、めんどくさい三角関数の計算が指数関数の計算に変わるので計算が楽になる。
(指数関数の計算がめんどくさいから対数を取るのと、感覚的には同じ考え方)
<研究>三角関数を指数関数であらわす
オイラーの公式より、
オイラーの公式の複素共役を取ると、
{(1) + (2)}/2 よりcosが、 {(1) - (2)}/2i よりsinが次のように求まる。
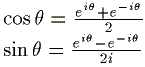
よって、三角関数は指数関数で表された。
http://ameblo.jp/neomanichaeism/entry-11344606343.html