さ~て、先日、ある資料を読んでいましたら、久し振りに『単調関数』と言う言葉に出会いました。
懐かしいな、と思った次第です。
そこで、本日は、小職の復習の意味も込めて、『単調関数』に関して見て参ります。
以下、日本大百科全書(ニッポニカ)に掲載されていた内容が分かりやすく思いましたので、転載させて頂きます。
尚、記述内容は、竹之内脩氏の手に成るモノです。
また、主旨が変わらない程度で、小職が書き換えています。
増加関数、減少関数をあわせていう術語。減少関数は、マイナスをつければ増加関数になるから、以下の説明では増加関数について述べる。
実数のある区間a≦x≦b(区間の片方、または両方の端が入っていなくても良い。
またa、bは±∞でもよい)において定義された実数値関数f(x)に対し、
x1<x2 ならば f(x1)≦f(x2)
である時、f(x)はこの区間で単調増加であると言う。
もし、ここで、つねにf(x1)<f(x2)である時は、単に増加(または狭義の増加)関数と言う。
例えば、
f(x)=x (-∞<x<+∞)
f(x)=x2 (x≧0)
などは増加関数である。
また、
f(x)=[x] (-∞<x<+∞)
ここで[x]はxの整数部分、すなわちxより大きくない整数のうちで最大のものを表す。[x]はガウスの記号とよばれている。
この様に全区間がいくつかの区間に分けられ、各小区間の上では定数値を取りながら増加して行く様な関数を階段関数と言う。
単調増加関数は次の様な性質を持つ。
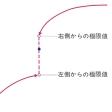
(1) 単調増加関数は、必ずしも連続ではないものの、不連続である点は、たかだか可算個で、不連続点においては、左側からの極限値、右側からの極限値を有する(図B)。
(2) 連続な増加関数は逆関数を有し、逆関数もまた連続、増加である。
(3) 単調増加関数は、ほとんどすべての点で、すなわちルベーグ測度が0であるような集合上を除いて微分可能である。
(4) f(x)がすべての点の上で微分可能で、f′(x)≧0ならばf(x)は単調増加である。
(5) 単調増加関数は、リーマン積分可能である。
(6) 区間[a,b]上の単調増加関数f(x)は、[a,b]上でフーリエ級数に展開できる。すなわち、そのフーリエ級数は、すべての点で収束し、f(x)の連続点では、その値はf(x)に等しい。これはフーリエ級数論において、ディリクレが印(しる)した第一歩であった(1829)。
単調増加関数の差として表される関数を有界変動関数と言う。これは次のような性質で特徴づけられる。c,d(c<d)を定義域のなかの任意の2点とすれば、ある正数Mがあって、
c=x0<x1<x2<……<xn=d
と言う様な点x1,x2,……,xn-1をどの様に取っても
|f(x1)-f(x0)|
+|f(x2)-f(x1)|
+……+|f(xn)-f(xn-1)|≦M
となる。
と言う事でした。面白いですよね。
では、本日の小職の予定です。
今日は、先ず、児童障碍者通所施設で、基礎的科学実験を実施して来ます。
今日は、高気圧及び低気圧出現の実演して来ます。子供達が愉しんでくれると良いですがね。
尚、上記の事が終わり次第、書斎に戻り、山積している書類と格闘します。
そして、今日は、昭和の日です。昭和天皇のありし日々を思い出しますね。